by Marcello Mamino
< Go to the previous post in the series
Emboldened by my success with problem 3, I move with confidence up the list. To be honest, this is exactly what I did, uncountable years ago, at the IMO. Even better, I then did problem 2 in a matter of minutes. Save discovering shortly after the competition that my solution was worth precisely nought, because I misread the statement. Certainly, that was an excess of boldness. Still, at that time, we considered 7-0-7 a decent result. And I put forward, in my defence, that I could not have solved that problem anyway. Let's see if history repeats itself (it won't: I would never confess in writing a blunder so gross). It's time for combinatorics.
EGMO 2013, problem 2. Determine all integers $m$ for which the $m\times m$ square can be dissected into five rectangles, the side lengths of which are the integers $1, 2, 3, \dotsc, 10$ in some order.
This is a typical search problem, I want to spend a few words about them. Suppose for a moment that the value of $m$ is fixed, then the problem would be stated as "is there a tiling of the $m\times m$ square$\dotsc$" which question has a similar structure to "is there a disposition of eight queens on a chessboard such that they don't attack each other?", or "can a chessboard without two opposite corners be covered by dominoes?". Notably, these questions do not ask for all configurations, and this suggests two different approaches. If the set of solutions is small or even empty, then one needs to analyze the hypothetical solutions very carefully, and often to fully describe the set: this is the case of the dominoes. If the set of solutions is large and rather unstructured, as for the eight queens, then the best approach is to try and construct one, by trial and error, a bit of intuition, and common sense. In either case, taking the wrong strategy might spell disaster. So this type of problems often involves some kind of alternation between an experimental mode and an analytic mode, and sticking to one would be ill advice.
My expectation, at first sight, is that only a few values of $m$ will matter, limited by the maximum possible area of the rectangles. For each of these $m$, I have a different search problem. I expect the ones that have solutions to be easy to solve by just some trial and error. After all, problem 3 has been so easy that this one must really be a piece of cake: I have no reason to expect any difficulty with the feasible cases. For the ones that can not be solved, there will be some colouring, or parity, or modular thing going on, like in the dominoes problem. So I have my strategy: first find the admissible values of $m$ with areas, second look for a few solutions by trial and error, third figure out which values don't have a solution and look for an invariant.
The maximum total area of our rectangles is clearly \[ A_{\textrm{max}} \;=\; 10\times 9 + 8\times 7 + 6\times 5 + 4\times 3 + 2\times 1 \;=\; 190\] and the minimum \[ A_{\textrm{min}} \;=\; 10\times 1 + 9\times 2 + 8\times 3 + 7\times 4 + 6\times 5 \;=\; 110\] Why? Well, it just looks right, and it is also almost the rearrangement inequality. I will not spend time looking for a proof until I have completed the rest of the solution, but I think it likely that an argument by induction, similar to that of the rearrangement inequality, will yield these bounds. If I need it in my solution, I will find it later, or, in zeitnot as a chess player would say, I will just pretend that these are well known facts. Anyway, I am left with just three values of $m$ to check, $11$, $12$, and $13$, which surprises me slightly because, at first, I had the impression of a greater variety of cases.
I did good progress so far, which makes me hope for a quick conclusion by just finding configurations for $m=11,12,13$. So I draw three little figures that look more or less like the one on the right: I will call this disposition of five rectangles in a square windmill configuration. I make sure to draw the rectangles of the figure for $m=11$ skinny and tall, and those of $m=13$ quite square-ish. I don't know whether or not there are other arrangements of the five rectangles to consider, however, for now, this one seems reasonable, so I hope to find solutions that look like this. Finally, I set out to find my configurations by writing numbers on the edges of the rectangles.
I spend most of the time of this blind search on the case $m=11$, somewhat less on $m=12$, I give up before even trying $m=13$. It might be bad luck, it might be that there are actually not so many solutions, but after a few minutes it becomes apparent that I am not going anywhere. Can I prune the search space somehow? I notice that the perimeter of the square, $4m$, needs to equal the sum of the dimensions of the four outer rectangles. This means that I can compute the sum of the dimensions of the inner rectangle by adding together all the sides, obtaining $1+2+\dotsb+10=55$, and then subtracting $4m$. This gives me $11,7,3$ respectively for $m=11,12,13$.
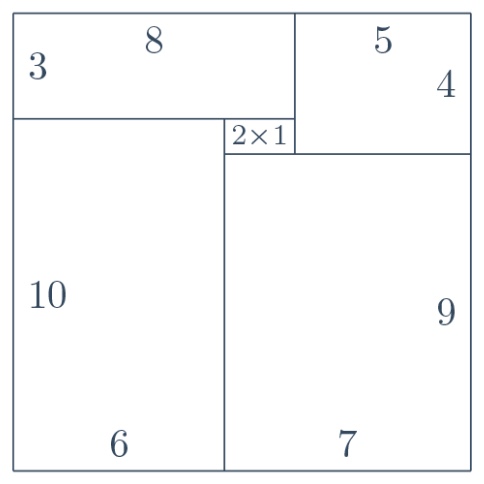My new observation seems more incisive for $m=13$, because, in this case, it leaves only one choice for the dimensions of the inner rectangle, namely $2\times 1$. I give it a try and, at the first attempt, with a bit of luck, I immediately hit upon a solution. (If you are curious to know how much luck did I actually use, it turns out that the likelihood was one in three. So it was not just a bit of luck, it was indeed about $1.58$ bits.) This is the configuration on the left of this paragraph. Unfortunately, my good luck does not hold for the other cases, so I set forth for more analysis.
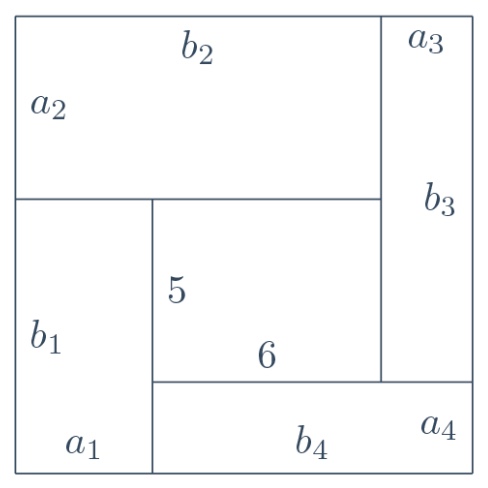I am still in the mood for finding solutions rather than proving that they don't exist, and I have a bad feeling about $m=12$: it's even. So I begin from $m=11$. I have various choices for the inner rectangle: $6\times 5,\, 7\times 4 \dotsc$ (sum$=11$). Starting from $6\times 5$, I make a list of the choices available for $a_1, a_2, a_3, a_4$ in the figure, subject to the constraint that $a_1+a_3=11-6=5$ and $a_2+a_4=11-5=6$.
My little table of choices now looks like this.
| $a_1+a_3$ | $2+3$ | $1+4$ |
| $a_2+a_4$ | $2+4$ | $1+5$ |
as you can see below the figure. On the line $a_2+a_4$ I didn't write $3+3$ because, of course, $a_2$ and $a_4$ need to be different. By the same principle, I can now cross out $1+5$ from the same line, because $5$ is already one of the sides of the inner rectangle. So I have established that $a_2$ and $a_4$ are $2$ and $4$, it doesn't matter in which order because $a_2$ and $a_4$ are exchanged by a rotation of the figure by $180^\circ$. Looking at the line $a_1+a_3$, I must now cross out the combination $2+3$, because $2$ is already used for $a_2$ or $a_4$. Similarly I cross out also $1+4$, because $4$ is used. So no option is left but to discard the whole case that the inner rectangle is $6\times 5$.
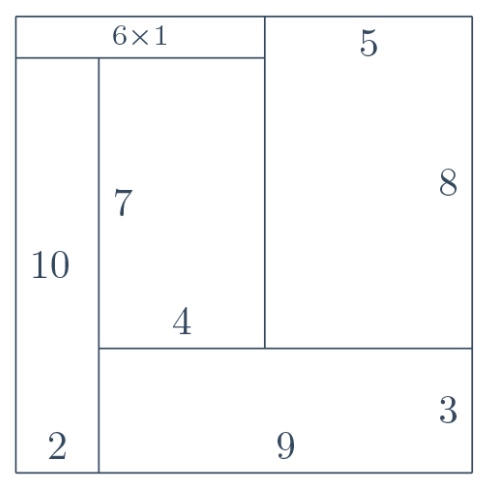The method of the little table is clearly general. I will not write here all the boring details, as anyone can turn that handle by himself; it suffices to say that, in the next case examined, $7\times 4$, all options cross out except one, which gives the solution on the left. Having found solutions for $m=11$ and $m=13$, I turn my method to $m=12$ and in short order I discard all combinations, thus excluding this case. Have I finally concluded problem $2$? Not yet, not even close$\dotsc$
I look back to what is missing, now, in my argument. Definitely I need to prove the inequalities, and that gives the impression of a merely technical exercise. Also I need to check whether there are other dispositions of rectangles besides the windmill configuration. This second gap might actually hold some surprise, so I decide to look into it first. Any tiling of the square needs to cover the four corners of it, and, since the side length of the square is larger than any of those of the rectangles, I can observe that two corners cannot be covered by the same rectangle. Now I want to say that the remaining rectangle is in the center. If not, it must be on one side, hence, on the opposite side, I have only two rectangles. I represent the situation like this.
They fit like a three-stepped peg in a two-stepped hole (observing that the steps are really three and two because all the side lengths of the rectangles are different). I conclude that the fifth rectangle can not be on one of the sides, as a consequence each of the four rectangles in the corners must touch those of the adjacent corners, and I am in the windmill configuration. Or am I?
I have stumbled upon the problem of balancing precision and practicality in mathematics. We all agree that correctness of a mathematical proof should be a purely logical matter. However, in practice, one can not trace back everything to the axioms of Euclid (or, better said, their modern substitutes). If for no other reason, at least for lack of space and time. In this particular case, I have no real definition of the windmill configuration, which makes it impossible to prove anything about it. Of course, I can identify it as a configuration such that precisely four of the rectangles touch the sides of the square. However, this is hardly a definition in the sense of allowing me to formally prove properties like $a_1+a_3=5$. But why? One definition is never an isolated entity. What does it mean to "touch the sides"? What is a "dissection of the square"? When do two polygons "overlap"? If I go down the rabbit hole, I will end up realizing that I don't even know what a rectangle is, or a number. Everyone must accept a reasonable level of imprecision, it might even be a necessity for effective communication. I satisfy myself with my imperfect definition because it achieves what is important: that the reader understands it clearly, and agrees that my conclusions are correct. Nevertheless, this windmill configuration is just the tiniest bit above my level of comfort with imprecision.
Now that the windmills are sorted (sort of), I need to focus on the areas. Honestly, the technique that I am most eager to use on those things is called avoidance. I search the information that I managed to collect for anything that could help me bound the side of the square. My attention is attracted by the sum of the dimensions of the inner rectangle, that I know to be $11,7,3$ for $m=11,12,13$. The next term of the series $11,7,3$ is obviously $-1$. Fine, the dimensions of the inner rectangle sum to $55-4m$, hence $55-4m>0$, and $m<13.75$. I dispensed with $A_{\textrm{max}}$, but, unfortunately, I cannot find anything like this to get rid of $A_{\textrm{min}}$ as well. Clearly $m\ge 10$, because $10$ is one of the dimensions of the tiles, but my proof of the windmill configuration relies on each corner of the square belonging to a different tile, which in turn requires $m>10$. So I can not use the windmill to exclude the case $m=10$, and, since essentially all that I have proven so far is based on the windmill configuration, here I am back to square one. After considering the idea of classifying more configurations, I decide that the most expedient course of action is to just prove the inequality.
I want to prove \[ A_{\textrm{min}} \;=\; 10\times 1 + 9\times 2 + 8\times 3 + 7\times 4 + 6\times 5 \;=\; 110\] my impression is that I need to generalize it and then prove it by induction. I choose the following generalization.
Let $x_1<x_2<\dotsb<x_{2n}$ be positive real numbers. Partition the set $\{x_1, x_2\dotsc x_{2n}\}$ into $n$ pairs $\{a_1,b_1\},\,\{a_2,b_2\}\dotsc$ Then \[ x_1x_{2n} + x_2x_{2n-1} + \dotsb \;\le\; a_1b_1 + a_2b_2 + \dotsb \]
Obviously I needed to replace $10$ with $n$. I decided to also replace the numbers with indeterminates because, otherwise, I might find myself embarrassed when, to make the inductive step, I remove the product $1\times 2n$ and I end up with the wrong set of numbers: $2\dotsc 2n-1$ instead of $1\dotsc 2(n-1)$.
The inductive step should be immediate. I assume the negation of the thesis \[ a_1b_1 + a_2b_2 + \dotsb \;<\; x_1x_{2n} + x_2x_{2n-1} + \dotsb \] If $x_1$ is paired with $x_{2n}$, I just erase the product $x_1x_{2n}$ thus contradicting the inductive hypothesis. So $x_1$ is not paired with $x_{2n}$, therefore, without loss of generality, I can assume $a_1=x_1$ and $b_2=x_{2n}$. Now it should happen that \[ a_1b_2 + a_2b_1 \;\le\; a_1b_1 + a_2b_2 \tag{$\star$} \] which, by the way, is case $n=2$. If this happens, then \[ a_1b_2 + a_2b_1 + \dotsb \;\le\; a_1b_1 + a_2b_2 + \dotsb \;<\; x_1x_{2n} + x_2x_{2n-1} + \dotsb \] and I have contradicted the hypothesis again because $a_1b_2$ is just $x_1x_{2n}$. To check ($\star$), I bring everything to the right hand side of the inequality \[ 0 \;\le\; a_1b_1 + a_2b_2 - a_1b_2 - a_2b_1 \;=\; (a_2 - a_1) (b_2 - b_1) \] and the two parentheses are positive because $a_1=x_1$ is the smallest of the indeterminates, and $b_2=x_{2n}$ is the largest.
Sonnez trompettes et clairons! I am finally out of this madness.
I have indeed completed a proof that I am confident, if competently written, would give me full points. Writing it up, however, is no easy task (and I can tell because, indeed, I did turn my thoughts into words, at least partially, in the paragraphs above). There is the death of a thousand cuts of the tables of cases to eliminate. There is all the handwavy arguing around windmills. There is the lemma of the inequality that needs to be formulated properly. And, also, I am not satisfied by bludgeoning through the problem in this way. A quick perusal of my tables of cases for $m=12$ shows an array of all possibilities, all neatly arranged, and all carefully crossed out. Arguably, this artifact is precisely as informative as a fresh table of all cases, all neatly arranged, no one crossed out. Since I need to reconstruct an argument anyway, I might as well look for a quick one. Indeed, I spend a moment looking for a simple way to do the exclusion of cases, and I find it. But really this is not what I want to do: I want to get rid of the windmills.
Now, in a competition, I would probably evaluate how much time I have left. Maybe I would turn my attention to another problem, and leave the write-up of this one for later. There are two benefits in finding a much shorter proof, or one that is considerably easier to write: the first is that it takes less time to write it, the second is that the probability of introducing errors is decreased. These benefits come at the cost of time to look for a better solution, and at the risk of not finding it. The optimal strategy is not easy to divine. Fortunately for me, I am in no competition, so I just carry on thinking about this problem. (I am also known to make very bad decisions in these matters. As a student, I remember factoring during some exam a polynomial of ridiculous degree, like $10$, just because I saw that I could do it. Well, it was a polynomial in two indeterminates, and I could have as well solved for the other one, which was of degree $2$.)
I need a parity or colouring argument to exclude $m=12$, but I wouldn't know how to use colouring here. By parity, I know that there is an even number of rectangles of odd area. In other words, if the numbers are paired $(a_1,b_1)\dotsc(a_5,b_5)$, either all the products $a_ib_i$ are even, or there are three even ones and two odd ones (four odds can be excluded because that would require eight of the numbers to be odd). To begin with, I want to look further into the first case. Checking modulo $4$, or perhaps a larger power of two, seems to be a good idea. I notice that \[ \textrm{even} \times \textrm{odd} \;\equiv\; \textrm{even} \quad \textrm{(mod $4$)}\] or, more precisely, $(2x)\times(2y+1)=4xy+2x\equiv2x$ modulo $4$. I assume that all the products are even, namely, without loss of generality, $a_1\dotsc a_5$ are even and $b_1\dotsc b_5$ are odd. Then I can write \[ a_1b_1 +\dotsb+a_5b_5 \;\equiv\; a_1+\dotsb+a_5 \;=\; 2+4+\dotsb+10 \;=\; 30 \;\not\equiv\; 12^2 \quad \textrm{(mod $4$)}\] This leaves me with the case of two odd and three even products.
I attack the second case with a similar method. There are two products of the form $\textrm{odd}\times\textrm{odd}$, this leaves one mixed product and two of the form $\textrm{even}\times\textrm{even}$. Clearly the congruence modulo $4$ ignores the $\textrm{even}\times\textrm{even}$ summands. Adding the observation that \[ \textrm{odd} \times \textrm{odd} \;\equiv\; \textrm{odd} + \textrm{odd} - 1 \quad \textrm{(mod $4$)}\] I quickly compute that the mixed product $\textrm{even}\times\textrm{odd}$ must satisfy $\textrm{even}-\textrm{odd}\equiv 1$ modulo $4$. However, I can't make any more progress, and I begin to suspect that one pairing such that the sum of the products is $12^2$ might exist. Eyeballing one approximation and then improving it, I get \[ 10 \times 4 + 6 \times 2 + 8 \times 3 + 9 \times 7 + 5 \times 1 \;=\; 12^2 \] Therefore the numbers alone do not exclude $m=12$.
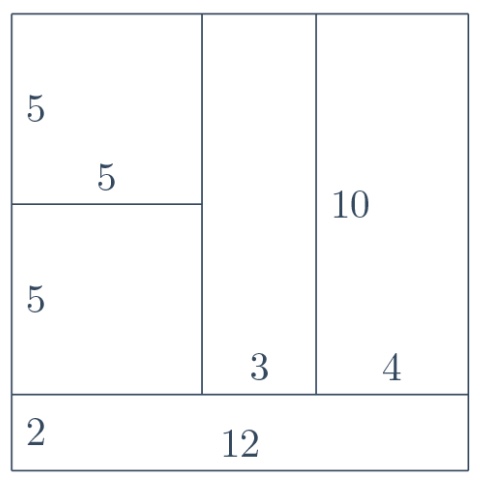I want a quick way to exclude configurations that have two $\textrm{odd}\times\textrm{odd}$ rectangles, two $\textrm{even}\times\textrm{even}$ rectangles, and a mixed one, for the case $m=12$. I immediately see a dissection of the $12\times12$ square into tiles that have the right parities (even though not the right dimensions), and indeed anyone can see it, here on the left. The existence of this configuration suggests to me that colouring arguments are not likely to work, definitely not one modulo $2$. Making this tiling, I had the impression that I could not have chosen the two $\textrm{odd}\times\textrm{odd}$ rectangles with dimensions that are all different. I felt forced to stack them one above the other as in the figure. This might lead to something, so now I am attracted by the idea of studying the relative position of the odd-sided tiles.
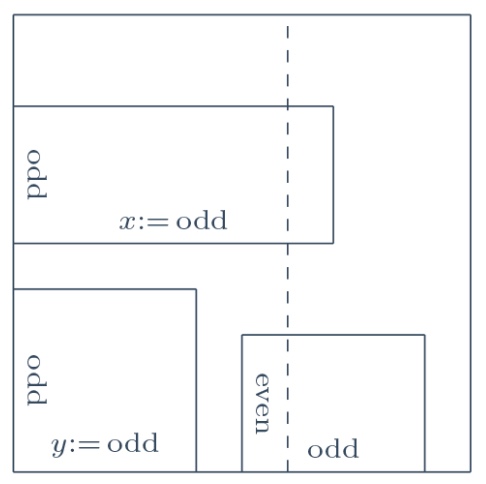One of the $\textrm{odd}\times\textrm{odd}$ rectangles must be in a corner of the square. No windmill here, just the good old pigeon hole principle. So the sides of the square that form that corner are divided by the tiles touching them into segments, at least one of which has odd length. Since $m=12$ is even, on each of these sides there must be another odd length segment, therefore each of the two remaining odd-sided tiles is adjacent to one of the sides of the corner. In the figure to the right, I put the corner to the bottom left, and I draw the side with the $\textrm{odd}\times\textrm{even}$ tile horizontally. I observe that, because $x\neq y$, I can draw a vertical line (dashed in the figure) that crosses one of the $\textrm{odd}\times\textrm{odd}$ tiles but not on the other. This line intersects each tile in an even length segment except one, which contradicts its length being even.
I have a new argument for the case $m=12$, and, what is better, I notice that one can clean it up substantially. Ignore the relative position of the tiles, and just call horizontal the direction of the odd side of the tile $\textrm{odd}\times\textrm{even}$. The intersection of a vertical line with any tile is a segment of even length, unless the tile is of type $\textrm{odd}\times\textrm{odd}$, in which case the segment has odd length. The horizontal lengths of the two $\textrm{odd}\times\textrm{odd}$ tiles differ, therefore one can find a vertical line that intersects just one of them, and this brings about the same contradiction as before. I am rather pleased with this argument, and I cannot fail to notice that it works for all even values of $m$, not just $12$. Beauty! I know very well that I was prompted to prove the $A_{\textrm{min}}$ inequality to exclude the single case $m=10$, so this new argument replaces also the inequality.
I quickly bring together my little armament. Of course $m\ge10$, and my latest advancement proves that $m$ is odd. The upper bound $m\le13$, however, still relies on $55-4m>0$, which was obtained as a consequence of those hellish windmills. At this point, I won't allow them to destroy my proof. I look into this $55-4m$, and it becomes presently apparent that the only observation required is that a tile can not have two opposite sides on the perimeter of the square. In fact, this implies that the perimeter of the square, which has length $4m$, is subdivided by the tiling into segments of distinct lengths between $1$ and $10$. Therefore $4m\le1+\dotsb+10=55$. I finally have an argument to be pleased with, read it just after this section.
The participants have obtained generally high scores on this exercise. In average 4.01 out of 7 points, median 5. I am confident that those of my readers that attempted the task did not fail. Personally, it took to me a marginally greater effort, compared with problem 3, to reach a first solution at the clarions. Writing that solution formally, which I didn't do, would have been quite time consuming. This problem then lingered in my mind for a few days, during which time I performed the remaining work piecemeal, often while doing something else, by mostly mental computation. Obviously I have no written record for this part, so it has been reconstructed in my narration, but I think faithfully.
I can't hide my satisfaction with the solution. In my opinion, it is a rather lovely argument. Comparison with the official solution shows that the key ideas of ours are completely different. The official solution, which argues through the windmill configuration and area inequalities, is remarkably well engineered. Even though it uses the windmill configuration, there is a visible effort to do it sparingly. In particular, it avoids the relations, such as our $a_1+a_3=5$, that connect the dimensions of the inner rectangle with those of the outer rectangles. These relations are, in fact, the hardest to justify formally, so I see it as an indication that its author, or authors, shared our same discomfort with windmills. The trick used in the official solution to deduce the $A_{\textrm{min}}$ and $A_{\textrm{max}}$ inequalities from rearrangement, instead of re-proving them, is really nice and worth remembering.
Solution to problem 2
Determine all integers $m$ for which the $m\times m$ square can be dissected into five rectangles, the side lengths of which are the integers $1, 2, 3, \dotsc, 10$ in some order.
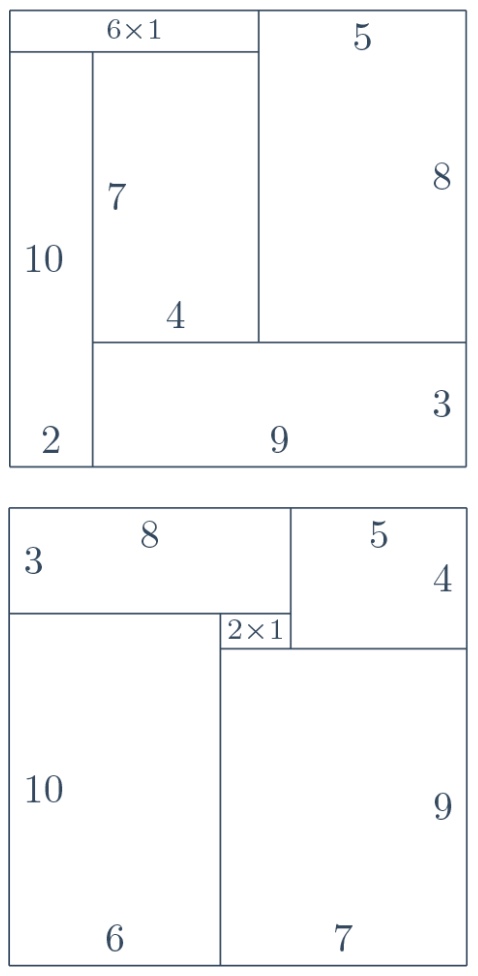
The values are precisely $m=11$ and $m=13$, and tilings for these values are exhibited in the figure. To exclude all other values, we begin with the observation that $m\ge10$, otherwise the tile having one side of length $10$ would not fit. Furthermore, we will prove that (a) $m\le 13$ and (b) $m$ is odd. This is enough to conclude.
For (a), assume $m\ge 14$. Observing that no tile can contact two opposite sides of the square, we conclude that the perimeter of the square, which has length $4m$, is subdivided by the tiling into segments of distinct lengths between $1$ and $10$. Therefore $4m\le1+\dotsb+10=55$, contradicting $m\ge 14$.
For (b), let $a_1\times b_1\dotsc a_5\times b_5$ be the tiles covering a square of even side length $m$. Since the area of the square must equal the total area of the tiles, either none or two of the products $a_ib_i$ are odd (four can be excluded because it would require eight of the dimensions to be odd). Considering the first case, by the pigeon hole principle, each product $a_ib_i$ contains one even factor and one odd factor: without loss of generality the $a_i$ are the even factors. Observe that \[ a_ib_i\; =\; a_i + a_i(b_i-1) \;\equiv\; a_i \quad \text{(mod $4$)}\] Therefore, computing the congruence modulo $4$ of the tiles' total area \[ a_1b_1 + \dotsb + a_5b_5 \;\equiv\; a_1 +\dotsb+ a_5 \;=\; 2 +\dotsb+10 \;\equiv\; 2 \quad \text{(mod $4$)}\] This contradicts $m^2$ being a multiple of $4$, thus excluding the first case. As a consequence, two of the products must be odd and three even. Hence two of the tiles are of type $\textrm{odd}\times\textrm{odd}$, one of type $\textrm{odd}\times\textrm{even}$, and two of type $\textrm{even}\times\textrm{even}$.
Call horizontal the direction of the odd side of the tile $\textrm{odd}\times\textrm{even}$. Any vertical line intersecting a tile must do it in a segment of even length, unless the tile is of type $\textrm{odd}\times\textrm{odd}$, in which case the segment is odd. The dimensions of all tiles differ, so do in particular the horizontal lengths of the two $\textrm{odd}\times\textrm{odd}$ tiles, hence we can find a vertical line intersecting one of them but not the other. This vertical line is divided into a union of segments precisely one of which has odd length, contradicting that $m$ is even. This excludes also the second case, thus establishing claim (b).
From xkcd by Randall Munroe (https://xkcd.com/556/)