Blog

  English version below / Vai alla versione italiana

This is part 5 of a series of posts on Maryam Mirzakhani’s story. You can find the previous installments here: part 1, part 2, part 3, part 4.

Admitted to the selective Sharif University, Maryam started regularly attending the Maths Circle - a circle of informal discussions made up of the best Iranian mathematicians of her generation. Meanwhile, her Olympic experiences continued, now as a trainer. Together with Roya, she would collaborate with the Iranian Olympic Committee: she would prepare the training material, invent new problems, and give problem solving classes to the new generations. Omid Amid, now a CNRS researcher at ENS in Paris, was one of her students at the time. Amid recalls an exceptional instructor, full of energy, who would communicate an infectious passion for math: “as a student it was a pleasant moment for me to listen to her sharing her passion for knowledge with us”, he said, “mathematics is a language of peace and beauty; to have such a passion for mathematics, one needs to be full of peace and beauty interiorwise: Maryam was such a person”. Of her long Olympic experience remains today a beautiful book in problem solving: Elementary Number Theory, Challenging Problems. Written together with Roya Beheshti and published in 1999, the book is currently the standard reference for the Iranian Olympic training, and it has made it to its 12th reprint.

Harvard

In 1999 Maryam applied and was admitted to Harvard University. In the US, she quickly learnt how to adjust to a new environment and to the culture of a country so different from hers. She faced (and overcame) many prejudices about her education and about her country: “I should say that the education system is not the way people might imagine here”, she said in an interview, “as a graduate student at Harvard, I had to explain quite a few times that I was allowed to attend a university as a woman in Iran”. In Sharif she had studied mainly algebra, combinatorics and problem solving; she had to learn quickly many subjects which were part of the standard math curriculum in the US. “She faced the same difficulties than the rest of us”, said her friend and coauthor Kasra Rafi, “but in a year or two she was beyond reach”. She started following Curt McMullen’s (a 1998 Fields Medalist) informal seminar, initially - as many graduate students - without understanding anything. In this regard she would say: “Well, most of the time I couldn’t understand a word of what the speaker was saying. But I could appreciate some of the comments by Curt”. She was captured by the beauty: “I was fascinated by how he could make things simple, and elegant. So I started asking him questions regularly, and thinking about problems that came out of these illuminating discussions.” McMullen, on his part, was impressed by Maryam’s imagination: “all students have questions, but her questions were unusually imaginative”, he said, ”Maryam's questions were more like mathematical short stories of her own invention, sometimes fictional but always intriguing”. He explained, “what she was trying to do was craft a narrative to make sense of the mathematical world that she was going to do research in”.

Thanks to McMullen, Maryam discovered the secret beauty of hyperbolic geometry.

The hyperbolic plane

The geometry we all learn in school is the Euclidean geometry. It is based on five postulates, elaborated by Euclid:

• A straight line segment can be drawn joining any two points. (Postulate I)
• Any straight line segment can be extended indefinitely in a straight line. (Postulate II)
• Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. (Postulate III)
• All right angles are congruent. (Postulate IV)  
• Given any straight line and a point not on it, there exists one and only one straight line which passes through that point and never intersects the first line. (Postulate V)

Can one prove Postulate V using only the first four postulates? The definitive answer to this ancient question arrived only in the nineteenth century: no, there do exist other geometries - other ways of thinking of the plane and its lines - where the fifth does not. The other geometries are called non-euclidean, and there are two of them: the spherical geometry and the hyperbolic geometry.

In spherical geometry the plane is thought of as a sphere, and straight lines as maximal circles. In this model only the second and the fourth postulate hold. Indeed, there are infinitely many lines between the North and the South poles and a sphere does not contain circles of arbitrarily great radius. Instead of Postulate V, the following holds:

•  Given any straight line and a point not on it, there exists no straight line which passes through that point and never intersects the first line.

In hyperbolic geometry the first four postulates still hold, while the fifth postulate does not, and is replaced by the following one:

• Given any straight line and a point not on it, there exist infinitely many straight lines which pass through that point and never intersect the first line.

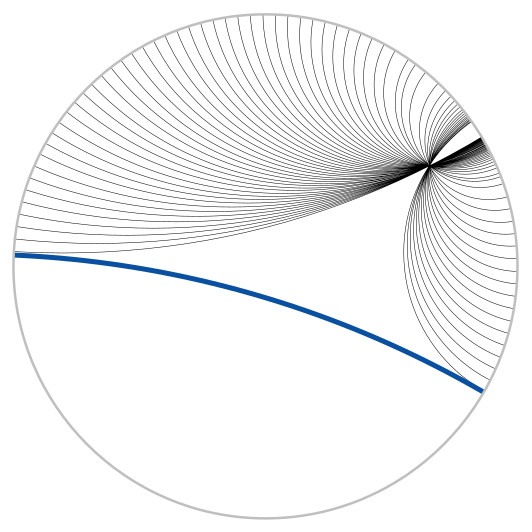
How does the plane look like according to hyperbolic geometry? There are several models, in the one elaborated by Poincaré the plane can be thought of as a disk and the lines as arcs of circles orthogonal to its boundary.

Poincaré’s disk, a blue line and several parallel lines through the same point.

Unlike Euclidean triangles, the sum of the angles of a hyperbolic triangle (in radians) is always smaller than pi. In the hyperbolic plane there are no rectangles, that is quadrilaterals with four right angles, the polygon with the fewest sides having all right angles is the hexagon. In order to draw a hyperbolic right-angled hexagon one needs to specify the measures of three edges which are pairwise non-adjacent.

A right-angled hyperbolic hexagon.

From the plane to hyperbolic surfaces

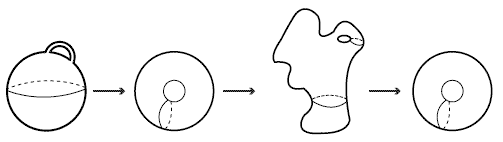
In mathematics a surface is a bi-dimensional object obtained by gluing together pieces of plane. Some of the simplest examples are the plane, the cylinder and the sphere. In general, one can imagine a surface to be like a sphere, possibly with “holes” and “handles”. It’s the number of “holes” and “handles” which classify the topology of a surface, that is its shape up to deformation.

Deforming a surface.

These surfaces have different topology.

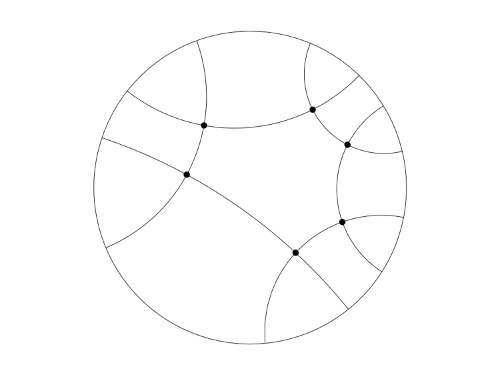
On the plane we can measure distances, areas, angles… We can do geometry! Can we do the same on a more complicated surface? The answer is yes, we can as long as we sew together polygons, which are “suited” to this purpose. In order to build a hyperbolic surface we sew together right-angled hyperbolic hexagons. The easiest one has the shape of a pair of pants. It goes as follows.

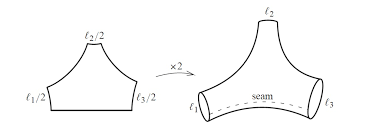
Pick two right-angled hyperbolic hexagons with the same side measures. Let us sew them together on alternates edges as in the figure.

Gluing together two right-angles hexagons into a hyperbolic pair of pants.

What we obtain is a hyperbolic pair of pants: each of the three boundaries is “smooth” - without corners - and twice as long as the edge of the hexagon we used. In this way we can construct a different hyperbolic pair of pants for each choice of the lengths  l_1, l_2 ed l_3. In the three cases, the shape of the surface stays the same - the one of a pair of pants -, while its measures, their hyperbolic structure, change. 

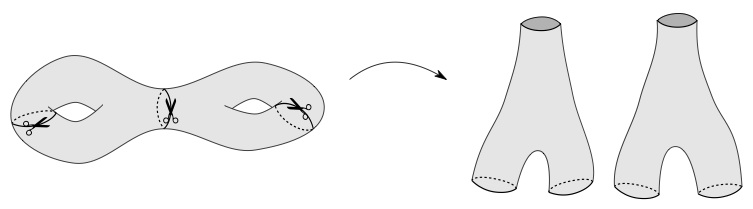
Gluing together hyperbolic pair of pants with compatible lengths, we obtain hyperbolic surfaces with more complicated shapes as here:

Gluing two pair of pants into a surface.

On the hyperbolic plane we know what the shortest curves between two points look like and we can compute their lengths. What happens, instead, on a hyperbolic surface? How do the shortest curves - its geodesics - of surfaces like the one above look?

The field of hyperbolic geometry deals with this sort of questions.

We said above that a pair of pants can have many different hyperbolic structures - one of every choice of the three “sizes” l_1, l_2 and l_3. But what happens in general?

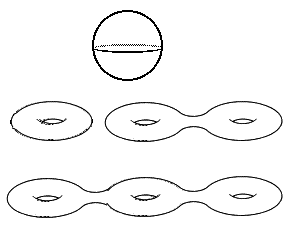
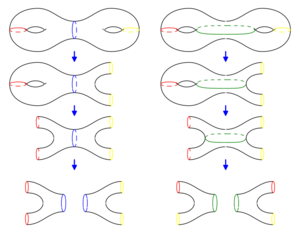
For instance, pick two identical hyperbolic pairs of pants and glue them in these two different ways:

Two ways of gluing two hyperbolic pair of pants which give two surfaces of the same shape.

We obtain two hyperbolic surfaces which have the same shape (a “doughnut with two holes”). Do the surfaces have the same “measures”? Are there other hyperbolic structures on a surface with that shape? 

The “catalogue” of all the possible hyperbolic structures on a surface of a given shape is called the moduli space. How does it look like? How “large” is this catalogue?

Computing the volume of the moduli space is a problem which intrigued many important mathematicians and physicists for decades, Maryam Mirzakhani was the first person who solved it completely.

Maryam Mirzakhani’s thesis

The starting point of Mirzakhani’s thesis was a beautiful formula discovered by Greg McShane about the lengths of simple closed geodesics on a hyperbolic surface which looks like a “holed doughnut”.

Both the red curves are simple geodesics: \(\gamma\) is closed; \(\tilde{\gamma}\) is not (the two extrema are asymptotically close, but they never touch each other).

Maryam understood how to use it to compute the volume of the moduli space of the surfaces with that shape. Moreover, she managed to generalize both the formula and her computation methods to surfaces of every shape. As an application of her work, she foundfinds a new proof of a famous conjecture by Gromov-Witten in string theory.

“Solving each problem would have been an event, and connecting them would have been an event” Benson Farb, professor at University of Chicago, says,  “and that’s what she did in her thesis.”

“But… what if it’s all wrong?” asked a worried graduate student Maryam to her friend Kasra Rafi as she was writing the papers related to her thesis.

But there was no mistake. Her works got accepted and published in the three best mathematics journals: Annals of Mathematics, Inventiones Mathematicae and Journal of the American Mathematical Society. What followed is an important page in the history of mathematics.

If you want to learn more about hyperbolic geometry, you can watch these videos.

  Versione italiana a seguire / Back to English

Questa è la quarta parte della serie di post sulla storia di Maryam Mirzakhani. I post precedenti sono: parte 1, parte 2, parte 3, parte 4.

Ammessa alla selettiva Sharif University, Maryam inizia a frequentare regolarmente il Math Circle - il circolo di discussioni informali del dipartimento - insieme a quelli che diventeranno i migliori matematici iraniani della sua generazione. La sua esperienza olimpica continua, ma ora come allenatrice. Insieme a Roya, collabora con il comitato olimpico iraniano: prepara il materiale di allenamento, inventa nuovi problemi e tiene corsi di problem solving alle nuove generazioni. Omid Amini, ora ricercatore CNRS alla ENS di Parigi, è fra i suoi studenti di allora. Amid la descrive come un’insegnante eccezionale, gentile, piena di energia e che trasmette una passione contagiosa per la matematica: “come studente è stato bello per me vederla condividere la sua passione per la conoscenza con noi”, dice, “la matematica è un linguaggio di pace e bellezza; per avere una tale passione per la matematica, bisogna essere pieni di pace e bellezza dentro: Maryam era così”. Per Maryam la matematica è soprattutto armonia e bellezza, “aveva un grande senso estetico”, dice, “credo che fosse parte della sua ricerca continua per la bellezza assoluta in matematica”. Della lunga esperienza resta oggi un bel libro di problem solving: Elementary number theory, challenging problems. Scritto insieme a Roya Beheshti e pubblicato nel 1999, il libro è a tutt’oggi il testo di riferimento standard per il training olimpico iraniano ed è alla dodicesima ristampa.

Harvard

Nel 1999 Mirzakhani viene ammessa ad Harvard University. Trasferitasi negli USA, impara presto ad adattarsi al nuovo ambiente e alla cultura di un paese molto diverso dal suo. A Sharif aveva studiato soprattutto algebra, combinatoria e problem solving; deve imparare alla svelta molte materie che invece sono nel curriculum standard dei bachelor americani. “Ha avuto le stesse difficoltà iniziali di tutti noi”, dice l’amico Rafi, “ma in un anno o due è riuscita a superare tutti quanti”. Segue i seminari informali di Curt McMullen, medaglia Fields e professore ad Harvard, inizialmente - come molti dottorandi - senza capirci assolutamente niente. A proposito dirà: “Beh, la maggior parte del tempo non capivo una parola di quello che diceva. Ma riuscivo ad apprezzare alcuni dei commenti di Curt.” È la bellezza della disciplina che la intriga: “mi affascinava il modo in cui riusciva a rendere le cose semplici ed eleganti. Cosi ho iniziato a fargli domande regolarmente, e a pensare ai problemi che venivano fuori da queste belle discussioni”. McMullen, da parte sua, è colpito dall’immaginazione di Maryam: “tutti gli studenti fanno domande, ma le sue erano insolitamente creative”, dice, “le domande di Maryam sembravano più piccoli racconti di matematica inventati da lei, a volte un po’ fantasiosi ma sempre molto interessanti”. Aggiunge, “quello che cercava di fare era costruire una narrazione per dare un senso al mondo matematico in cui stava per fare ricerca”.

Grazie a McMullen, Maryam scopre piano piano la bellezza della geometria iperbolica.

Il piano iperbolico

La geometria che tutti studiamo a scuola è la geometria euclidea. Questa si basa su cinque postulati, formulati da Euclide:   

• per ogni coppia di punti passa un’unica retta (Postulato I);   
• ogni segmento si può prolungare a piacere (Postulato II);
• si possono disegnare cerchi di qualunque raggio e qualunque centro (Postulato III);
• tutti gli angoli retti sono congruenti fra loro (Postulato IV);
• dati una retta e un punto esterno ad essa, si può tracciare un’unica retta che passa per il punto e non interseca la retta data (Postulato V).

Si può dimostrare il Postulato V utilizzando solo gli altri quattro? La risposta definitiva a questa antichissima domanda è arrivata solo nel diciannovesimo secolo: no, esistono anche altre geometrie - altri modi di pensare il piano e le rette - in cui non vale il quinto postulato. Le altre geometrie, dette non-euclidee, sono due: la geometria sferica e la geometria iperbolica.

In geometria sferica il piano viene immaginato come una sfera, e le rette come cerchi massimi. In questo modello valgono solo il secondo ed il quarto postulato. Infatti, una sfera non può contenere cerchi di raggio troppo grande e tutti i cerchi massimi si intersecano nei due poli Nord e Sud (quindi ci sono infinite “rette” che passano per questi due punti).

Invece del Postulato V, vale il seguente:

• Data una retta e un punto, non esistono rette che passano per quel punto e non intersecano la retta data.

Nella geometria iperbolica valgono tutti i primi quattro postulati, mentre il Postulato V è falso. Vale invece il seguente:

• Dati una retta e un punto esterno ad essa, esistono infinite rette che passano per il punto e non intersecano la retta data. (Postulato V’)

Com’è fatto il piano secondo la geometria iperbolica? Ci sono diversi modelli, in quello elaborato da Poincaré il piano è pensato come un disco e le rette come archi di circonferenza ortogonali al suo bordo (vedi la figura ).

Il disco di Poincaré, una retta blu e molte linee parallele che passano per lo stesso punto.

A differenza dei triangoli euclidei, la somma degli angoli di un triangolo iperbolico è sempre inferiore a pi. Nel piano iperbolico non esistono rettangoli, cioè quadrilateri con quattro angoli retti, il più piccolo poligono con tutti gli angoli retti è l’esagono. Per disegnare un esagono iperbolico retto basta specificare le misure di tre lati a due a due non adiacenti.

Un esagono iperbolico rettangolo.

Dal piano alle superfici iperboliche

In matematica una superficie è un oggetto bidimensionale ottenuto incollando insieme dei pezzetti di piano. Gli esempi più semplici sono il piano, il cilindro e la sfera. In generale si può immaginare una superficie come una sfera, magari con dei “buchi”, a cui sono attaccati dei “manici”. È proprio il numero di “manici” e di “buchi” che classifica le superfici, a meno di deformazione.  

Deformare una superficie.

Queste superficie hanno diverse topologie.

Sul piano possiamo misurare le distanze, le aree, gli angoli, … Possiamo, insomma, fare geometria! Si può fare la stessa cosa su una superficie più complessa? La risposta è sì, basta cucire insieme dei poligoni “adatti” allo scopo. Per costruire una superficie iperbolica si cuciono insieme degli esagoni iperbolici retti. Quella più semplice da costruire è a forma di pantalone. Procediamo così.

Prendiamo due esagoni iperbolici retti con le stesse misure. Cuciamoli insieme sui tre lati alterni come in figura.

<

Incollare tra loro due esagoni rettangoli per ottenere un paio di pantaloni iperbolici.

Quello che otteniamo è un pantalone iperbolico: ognuno dei tre bordi è “liscio” - non ha spigoli - e lungo il doppio del lato dell’esagono da cui è stato ottenuto. In questo modo possiamo costruire un pantalone iperbolico diverso per ogni scelta delle lunghezze l_1, l_2 ed l_3. In tutti i casi, la “forma” della superficie resta sempre la stessa - quella di un pantalone - sono le sue “misure”, cioè la sua struttura iperbolica, a cambiare.

Incollando insieme pantaloni iperbolici con lunghezze compatibili, otteniamo delle superfici iperboliche dalla forma più complessa, come qui sotto.

Incollare due paia di pantaloni su una superficie.

Sul piano iperbolico sappiamo come sono fatte le curve più brevi fra due punti, sappiamo calcolarne la lunghezza. Cosa succede, invece, su una superficie iperbolica? Come sono fatte le curve più brevi - le geodetiche - di una superficie come quella della figura sopra?

Chi studia geometria iperbolica si occupa proprio di questo tipo di domande.

Abbiamo detto sopra che una superficie a forma di pantalone può avere tante strutture iperboliche diverse - una per ogni scelta delle tre “taglie” l_1, l_2 ed l_3. Ma cosa succede in generale? 

Per esempio, prendiamo due pantaloni iperbolici identici e incolliamoli in due modi diversi come nella figura qui sotto.

Due modi di incollare tra loro due paia di pantaloni iperbolici che danno luogo a due superficie della medesima forma.

Otteniamo due superfici iperboliche che hanno la stessa forma (a “ciambella con due buchi”). Le due superfici avranno anche le stesse “misure”? Quali altre strutture iperboliche possiamo costruire su una superficie di quella forma?

Il “catalogo” di tutte le strutture iperboliche possibili su una superficie di una forma prestabilita si chiama spazio dei moduli. Com’è fatto e quanto è “grande” questo catalogo?

Calcolare il volume dello spazio dei moduli è un problema che appassionato importanti matematici e fisici per decenni, sarà Maryam Mirzakhani a risolverlo completamente.  

La tesi di Maryam Mirzakhani

Il punto di partenza della tesi di Mirzakhani è una bella formula trovata da Greg McShane sulle lunghezze delle geodetiche semplici chiuse di una superficie iperbolica a forma di “ciambella bucata”.

Le due curve rosse sono entrambe geodetiche semplici: \(\gamma\) è chiusa; \(\tilde{\gamma}\) non lo è (i due estremi si avvicinano all’infinito ma non si toccano mai)

Maryam capisce come utilizzarla per calcolare il volume dello spazio dei moduli delle superfici di quella forma. Di più, riesce a generalizzare sia la formula che il metodo di calcolo a superfici di qualsiasi forma. Come applicazione del suo lavoro, trova una nuova dimostrazione di una congettura di Gromov-Witten in teoria delle stringhe.

“Risolvere anche uno solo di questi problemi sarebbe stato un evento, trovare un legame fra loro sarebbe stato un evento” dice Benson Farb, professore alla University of Chicago “e questo è quello che lei è riuscita a fare nella sua tesi”. 

“Ma… e se fosse tutto sbagliato?” chiede una Maryam dottoranda preoccupata all’amico Kasra Rafi mentre prepara i tre articoli relativi al materiale della tesi.

Ma non c’è nessun errore. I suoi lavori vengono accettati dalle tre migliori riviste di matematica mondiali: Annals of Mathematics, Inventiones Mathematicae e Journal of the American Mathematical Society. Il resto è storia della matematica.

Per saperne di più sulla geometria iperbolica, potete guardare questi video (in inglese).