Blog

  English version below / Vai alla versione italiana

This is part 4 of a series of posts on Maryam Mirzakhani’s story. You can find the previous installments here: part 1, part 2, part 3.

One day, Maryam found by chance the problem sheet of the National Informatics Olympiads. The competition was intended for older students; the time allowed was three hours. Maryam and Roya spent days thinking about the problems, eventually they managed to solve three exercises out of six by themselves. Amused, they asked the principal of the school for permission to take problem solving-classes and to participate in the competitions, as was the case in boys' schools. “The principal of the school was a very strong character”, Mirzakhani said, “If we really wanted something, she would make it happen”.

At the end of the first year of high school, the 15-year-old Maryam and Roya performed so well that they were invited to the Math Camp at Sharif University - a summer workshop usually aimed at brilliant students one year older. Despite the many restrictions the regime imposed on girls - such as, for instance, the dress code and gender segregation in schools - Roya and Maryam did not perceive any prejudice on their abilities; quite the opposite, they felt strongly encouraged by their teachers. Roya said “I actually never felt I was at a disadvantage being a female student in the team”, and she explained that it was partly “because of all the encouragement that we got from the professors who were running the math camps, part of it was because I was with Maryam and it felt empowering to be with another female student, especially someone as strong as her.” Maryam and Roya stood out immediately thanks to the perceptiveness of their questions and their enthusiasm. Ebad Mahmoodian, professor at Sharif University, was among the teachers at the workshop. He presented to the students an open problem in graph theory.

A graph (Image by User:AzaToth via Wikimedia Commons)

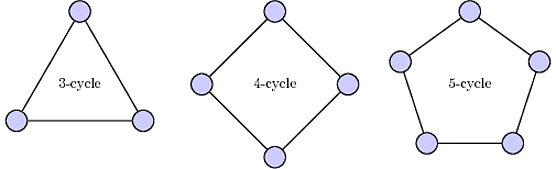
A cycle (Image by Douglas S. Stones on MathStackexchange)

In mathematics, a graph is just a set of vertices (nodes) and edges. For instance, a family of graphs easy to describe is given by cycles: a n-cycle is a graph made of n vertices on a closed path. Decomposing a graph G means describing it as a union of “simpler” graphs such that each edge of G belongs to exactly one graph in the decomposition. In general, understanding whether a given graph can be decomposed in graphs with certain properties is a very difficult problem. For instance, some graphs can be decomposed as a union of cycles, others can’t.

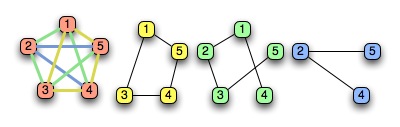
Decomposition of a graph. (Image by  Mark C. Chu-Carroll on Scienceblogs)

The problem asked by Mahmoodian at the Math Camp is about graph decompositions: find necessary and sufficient conditions for the decomposition of a (complete and tripartite) graph into 5-cycles. As a first step, he suggested the students to build an example of such a graph. As it was a very difficult exercise for 15-year-old students, he offered a $1 prize for every example they could find. An amused Mahmoodian recalled that after a couple of lectures Maryam discovered an infinite family of graphs with this property. Deeply impressed, he invited her to work together on the problem at Sharif University.

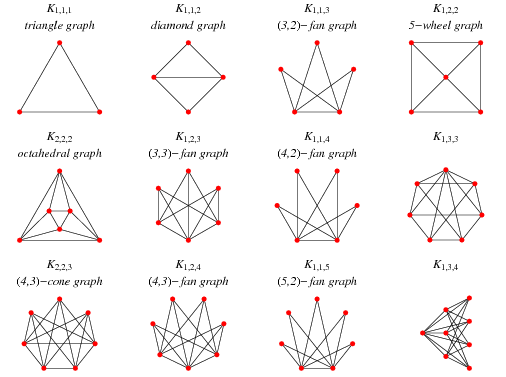
Complete tripartite graphs. (image from Wolfram Mathworld)

Mahmoodian successfully urged the Iranian Olympic Committee to admit her and Roya to the National Math Olympiad the next year, in their 10th grade, rather than in their 11th grade, as was required by the old regulation. The principal of Maryam’s school was totally enthusiastic about the fact that Maryam and Roya could train with him at Sharif, and she hoped that maybe they might join the Iranian Olympic Team - no girl had ever done that before. She supported them as much as she could, organizing problem solving lectures for them given by former team members. “Her mindset was very positive and upbeat that ‘you can do it, even you'll be the first one’”, Mirzakhani said, “I think that has influenced my life quite a lot.” The training with Mahmoodian bore fruit: Maryam eventually solved the problem asked at the Math Camp. The solution is the object of the paper “Decomposition of complete tripartite graphs into 5-cycles” written together with Mahmoodian and published in 1995. In 1994, the 17-year old Maryam and Roya would be the first girls to join the Iranian Olympic team for the IMO in Hong Kong. They achieved extraordinary results: Maryam won a gold medal with 41/42 and Roya a silver medal with 35/42.

The next year, she continued her training in Sharif. Kasra Rafi, her future collaborator and now associate professor at University of Toronto, and Saieed Akbari, now professor at Sharif University of Technology, were among her instructors. Rafi says: “It was a challenge to find something that she couldn’t solve”, remembers how he, undergraduate student at the time, even happened to learn new mathematics by just correcting Maryam’s solutions. During his training sessions Akbari, just graduated in combinatorics, would ask the students difficult problems in graph colorings.

Given a graph, a colouring is a way of assigning a colour to each vertex such that any two adjacent vertices have a different colour. A graph is k-colourable if it admits a colouring made of k colours: here we see a 3-colourable graph.

A 3-colourable graph. (Image Wikimedia Commons)

How do we know if a given graph is k-colourable or not? In general, even when k=3, the problem is very difficult from a computational point of view - it is classified as NP-hard. There are many variations of this problem. One of this considers graphs, which we call k-choosable, where each vertex is associated to a list of k colours with some properties. An example of a non 3-choosable graph is given in the next figure.

A non 3-choosable graph. (Image by David Eppstein from Wikimedia Commons)

In 1993 Margit Voigt had built an example of a planar graph non 4-choosable: her example has 238 vertices. Saieed Akbari was an expert in graph theory and knew Voigt’s work; he also knew it was a difficult problem. He decided to give it to the Iranian team as an exercise anyway, offering $10 to those who could solve it: “If I had offered $100, nobody would have ever tried”. After some days, Maryam met him in the hall and handed him a one-page hand-written solution of the problem. Maryam’s example had only 69 vertices, and moreover it was also 3-colourable: not only was her example easier than Voigt’s, but it was a counterexample to a known conjecture as well. Akbari was surprised and incredulous when he received Maryam’s solution, which he carefully checked overnight. The next day he gave her the sheet back with the comment: “I find it really beautiful and creative!!!”. There were no errors, and the proof would become a paper, published in 1996 in BICA, and still frequently cited among the experts. At the end of the training, Maryam was the bright star of the Iranian team at the 1995 IMO; she won a gold medal again, this time with a perfect score (42/42), and she became a celebrity in Iran.

In the beginning, mathematics was just a game to Maryam, but, thanks to the beautiful Olympic experience and to the people she met, the game turned into a passion. “As a teenager, I enjoyed the challenge. But most importantly, I met many inspiring mathematicians and friends at Sharif University”, she said, “the more time I spent on mathematics the more excited I became”. Noohi Behrang, her former trainer for the IMO, now Reader at the Mathematics Department of Queen Mary University of London, remembers her not only for her talent and passion for mathematics and science, but also for her sensitivity and beautiful human qualities. “She told me that she wanted to continue math at the university because she found mathematicians nice people”, he said, “she loved math but at the same time she would see the human side of it, the kindness and the niceness of the people there was important to her”, he explained, “and she was indeed an example of a kind and nice person.”

TO BE CONTINUED

If you are looking for a challenge, here are the problems from the two IMO Maryam Mirzakhani took part in: IMO 1994, IMO 1995.

A (quite technical) report on Mirzakhani’s early papers: On an early paper of Maryam Mirzakhani.

  Versione italiana a seguire / Back to English

Questa è la quarta parte della serie di post sulla storia di Maryam Mirzakhani. I post precedenti sono: parte 1, parte 2, parte 3.

Un giorno, Maryam trova per caso le domande delle olimpiadi nazionali di informatica di quell’anno. La competizione è rivolta a ragazzi più grandi; il tempo a disposizione per lo svolgimento dei problemi è di tre ore. Maryam e Roya passano giorni interi a ragionarci su, e alla fine risolvono da sole tre esercizi su sei. Divertite dal nuovo gioco, chiedono alla direttrice di poter seguire dei corsi di problem solving e partecipare alle gare anche loro, come già avviene nelle scuole maschili. “La direttrice della scuola aveva un carattere molto forte”, Mirzakhani dirà più tardi, “se davvero volevamo fare qualcosa, lei l’avrebbe reso possibile”.

Alla fine del primo anno di scuola superiore, le quindicenni Maryam e Roya sono così brave da essere invitate al Math Camp della Sharif University - un stage estivo normalmente rivolto a studenti brillanti un anno più grandi. Malgrado le molte restrizioni imposte dal regime alle ragazze - ad esempio, il codice di abbigliamento e la segregazione scolastica - Roya e Maryam non percepiscono alcun pregiudizio sulla loro intelligenza, anzi, si sentono molto incoraggiate dai loro insegnanti. “Non mi sono mai sentita particolarmente svantaggiata in quanto ragazza nel gruppo”, spiega Beheshti, “in parte grazie all'incoraggiamento degli insegnanti, in parte perché ero con Maryam, era bello essere lì con un'altra ragazza, soprattutto con una brava come lei”. Maryam e Roya si fanno notare subito per la perspicacia delle loro domande e per il loro entusiasmo. Ebad Mahmoodian, professore alla Sharif University, è fra gli insegnanti e durante il campo propone ai ragazzi un problema aperto di teoria dei grafi.

Un grafo (Immagine di User:AzaToth via Wikimedia Commons)

Un ciclo (Immagine di Douglas S. Stones su MathStackexchange)

In matematica, un grafo è semplicemente un insieme di vertici (nodi) e lati ciascuno dei quali connette due vertici. Per esempio, una famiglia di grafi molto facile da descrivere è quella dei cicli: un n-ciclo è un grafo formato da n vertici disposti su un cammino chiuso. Decomporre un grafo G significa descriverlo come una unione di grafi più “semplici” in modo tale che ogni lato di G appartenga ad uno solo dei grafi della decomposizione. In generale, può essere molto difficile capire se un dato grafo ammette una decomposizione in grafi con certe proprietà: tornando all’esempio di prima, alcuni grafi possono essere decomposti come unioni di cicli, altri no.

Decomposzione di un grafo. (Immagine di Mark C. Chu-Carroll su Scienceblogs)

Quello proposto da Mahmoodian al Math Camp è proprio un problema di decomposizione: trovare condizioni necessarie e sufficienti per decomporre un grafo di una certa famiglia (un grafo completo tripartito) in 5-cicli. Come primo passo, agli studenti viene chiesto di costruire un esempio di grafo che abbia tutte le proprietà richieste. Visto che si tratta comunque un esercizio molto difficile per dei quindicenni, il professore offre un premio di un dollaro per ogni esempio trovato. Mahmoodian racconta, divertito, che dopo un paio di lezioni Maryam scopre una famiglia infinita di grafi con questa proprietà. Profondamente colpito, le propone di continuare a studiare il problema aperto assieme a lui, a Sharif University.

Grafi tripartiti completi. (Immagine da Wolfram Mathworld)

Mahmoodian insisterà con successo presso il Comitato Olimpico Iraniano affinché lei e Roya possano partecipare alle olimpiadi nazionali di matematica già l’anno successivo, in seconda superiore, invece che in terza come previsto dal vecchio regolamento. La preside della scuola di Maryam è assolutamente entusiasta all'idea che Maryam e Roya possano allenarsi con lui a Sharif e spera che magari possano entrare nella squadra olimpica iraniana - nessuna ragazza ne aveva mai fatto parte. Fa loro avere tutto il supporto possibile, organizzando per loro anche dei corsi di problem solving tenuti da ex-olimpionici. “Aveva un atteggiamento molto ottimista e positivo ‘ce la puoi fare, anche se sarai la prima’”, ricorda Mirzakhani in una intervista, “credo che mi abbia parecchio influenzato nella mia vita.” Gli allenamenti con Mahmoodian danno i suoi frutti e Maryam riesce a risolvere il problema del Math Camp: la soluzione è contenuta nell’articolo “Decomposition of complete tripartite graphs into 5-cycles” scritto insieme a Mahmoodian e uscito nel 1995. Nel 1994 le diciassettenni Maryam e Roya saranno le prime ragazze ad entrare nella squadra olimpica iraniana e a partecipare alle IMO a Hong Kong. Ottengono risultati fenomenali: Maryam vince una medaglia d’oro con 41/42 e Roya una medaglia d’argento con 35/42.

L’anno seguente Maryam continua gli allenamenti a Sharif. Fra i suoi istruttori ci sono Kasra Rafi, suo futuro collaboratore e ora professore associato a University of Toronto, e Saieed Akbari, ora professore a Sharif University of Technology. Rafi ricorda: “era difficile trovare un problema che non sapesse risolvere” e ricorda di come lui, ai tempi già studente universitario, abbia persino imparato dei teoremi nuovi correggendo le soluzioni ai problemi trovate da una Maryam ancora liceale. Durante una sessione di allenamento Saieed Akbari, ai tempi fresco di dottorato in combinatoria, si diverte a proporre agli studenti dei problemi difficili sulle colorazioni dei grafi.

Dato un grafo, una sua colorazione è un modo di assegnare un colore ad ogni suo vertice in modo tale due vertici adiacenti siano sempre di colore diverso. Un grafo è k-colorabile se ammette una colorazione fatta da k colori: qui in figura vediamo un grafo 3-colorabile.

Un grafo 3-colorabile. (Immagine Wikimedia Commons)

Come si fa a capire se un certo grafo è k-colorabile o no? In generale, anche quando k=3, si tratta di un problema computazionalmente molto difficile, tanto da essere classificato come NP-hard. Esistono molte varianti del problema classico, una delle quali prende in considerazione dei grafi - detti k-sceglibili - in cui ad ogni vertice è assegnata una lista di k colori che deve soddisfare certe proprietà. Un esempio di grafo non 3-sceglibile è dato qui di seguito.

Un grafo non 3-sceglibile. (Immagine di David Eppstein da Wikimedia Commons)

Nel 1993 Margit Voigt costruisce un primo esempio di grafo planare non 4-sceglibile: il suo esempio ha ben 238 vertici. Saieed Akbari, un esperto di teoria dei grafi, conosce il lavoro di Voigt e ne capisce la difficoltà. Decide lo stesso di assegnare il problema come esercizio di allenamento agli studenti della squadra iraniana, offrendo 10 dollari in premio per la soluzione: “Se avessi offerto 100 dollari, nessuno ci avrebbe mai provato”. Dopo qualche giorno, Maryam lo incontra in corridoio e gli dà una paginetta scritta a mano con la sua soluzione. L’esempio di Maryam ha solo 69 vertici, ed in più è anche 3-colorabile: non solo l’esempio è più semplice di quello di Voigt, ma è anche un bel controesempio ad una nota congettura nel campo. Akbari accoglie la cosa con sorpresa e incredulità e controlla la soluzione nei minimi dettagli la sera stessa. Il giorno seguente le restituisce il suo foglietto con il commento: “La trovo davvero creativa e bella!!!”. Non c’erano errori e la dimostrazione si trasformerà in un articolo, pubblicato nel 1996 su BICA e tuttora abbastanza citato fra gli esperti del settore. Al termine degli allenamenti, Maryam è la punta di diamante della squadra iraniana alle IMO 1995; otterrà una medaglia d’oro, questa volta con punteggio perfetto (42/42) che la farà diventare una celebrità in Iran.

Maryam aveva iniziato ad interessarsi alla matematica per gioco, ma grazie alla bella esperienza olimpica e alle persone incontrate il gioco si è ormai trasformato in passione: “da adolescente, mi piaceva la sfida. Ma ciò che conta di più, ho incontrato molti matematici e amici a Sharif University che mi hanno ispirato”, dirà, “più tempo passavo a fare matematica più ero contenta”. Noohi Behrang, ora Reader al Mathematics Department of Queen Mary University of London e suo ex-allenatore per le IMO, la ricorda non solo per il talento e la passione per la matematica e le scienze, ma anche per la sensibilità e le belle qualità umane. “Mi ha detto che voleva continuare a studiare matematica all’università perché trovava i matematici persone piacevoli”, dice, “amava la matematica ma allo stesso tempo ne vedeva il lato umano, la simpatia e la bontà delle persone erano cose importanti per lei”, continua, “e lei era certamente una persona simpatica e buona”.

CONTINUA

Per chi volesse una sfida, qui ci sono i problemi delle IMO cui Maryam Mirzakhani ha preso parte: IMO 1994, IMO 1995.

Un report (piuttosto tecnico) sui primi articoli di Mirzakhani: On an early paper of Maryam Mirzakhani.