Blog

by Marcello Mamino

When Alessandra sent around an e-mail looking for contributors to this series, I had already solved most of past EGMO problems. It is tempting to reconstruct solution paths retrospectively, but, doing so, one goes at risk, in all honesty, of producing unnaturally elegant solutions, and also of forgetting the most embarrassing blunders. Fortunately, I noticed that I didn't tackle yet any of the three problems of Day 1 EGMO 2013, so I set out to do them from the point of view of a contestant. I took this as a sort of psychological experiment, so I will describe my solution process as it happened, and not as it could or should have happened.

To obtain the best instructional value out of this experiment, if you are not already familiar with the problems, I suggest that you solve them before going any further. Unfortunately, it happens at times that one problem just won't give. In this predicament, if you can say on your honour that it resisted a most gallant assault, then don't hold yourself vanquished. Read, instead, the relevant section just until a new idea comes up, and then stop to try again. Good luck!

Let's do the bold thing and start from problem 3.

EGMO 2013, problem 3. Let $n$ be a positive integer.

1. Prove that there exists a set $S$ of $6n$ pairwise different positive integers, such that the least common multiple of any two elements of $S$ is no larger than $32n^2$.
2. Prove that every set $T$ of $6n$ pairwise different positive integers contains two elements the least common multiple of which is larger than $9n^2$.

There are two parts, and if there is any dependency between the two, then it's going to be (b) depending on (a), so I should better start from (a). It wants me to build a large set $S$ of positive integers with small pairwise lcm.

Intuitively, elements of $S$ should have common factors, to keep the lcm low. So I suspect that $S$ might be something similar to the set of products $p_1^{e_1}\cdot p_2^{e_2}\dotsb$ with small primes $p_i$ and some balancing act to be performed on the exponents. Before I embark on something so complicated, I want to check the most trivial cases to set a baseline. For instance, what happens if I take the set of the first $6n$ numbers? Well, obviously the lcms are bounded by little less than $36n^2$: not so far off considering that I am only aiming for $32n^2$.

These numbers need to have some common factor, so what if instead of taking the first, say, $a$ numbers, I take the first $a$ even numbers? Clearly my bound on the lcms jumps from $a^2$ to $2a^2$, and that's a loss, the corresponding gain is that, now, I freed up all the odd numbers. To make a rough first attempt, I want to see what happens adding to $S$ those odd numbers that are halves of even numbers already in: clearly they cannot produce any larger lcm. My new $S$ contains $a$ even numbers and $\frac{1}{2}a$ odd numbers, total $\frac{3}{2}a$, so the square of the cardinality of $S$ has gone up by a factor of $\frac{9}{4}$ at the expense of increasing the largest lcm by a factor of $2$: that's a win.

I'm making some progress: even numbers are good. I want to check multiples of $3$ now. So I have the first $a$ multiples of $3$, namely all up to $3a$. In addition to these $a$ numbers, I have the non-multiples up to $\frac{1}{3}$ of $3a$, which makes a grand total of $\frac{5}{3}a$ numbers. My upper bound on the lcms is $3a^2$, and this means a loss of $3$ for a gain of $\frac{25}{9}<3$: not good.

I'm back to the multiples of $2$. First, I want to see how far I am from the goal. I take $a$ even numbers, namely up to $2a$, and $b$ odd numbers, namely below $2b$. I chose $a=2b$, and from $a+b=6n$ follows $b=2n$. My lcms are now bounded by more or less $2a^2=32n^2$. Surprising: it seems that this is already the solution. Or almost the solution, maybe I have ignored some $+1$ in the counts and that's where the devil is. So let's be precise. \[ S = \{ \text{even nrs.} \le 8n \} \cup \{ \text{odd nrs.} < 4n \} \]The lcm is definitely no larger than $32n^2$, the first set has $4n$ elements, the second $2n$. Fine: part (a) solved.

Part (b). From part (a) I have got some intuition about the critical $S$, the largest one having all lcms below $9n^2$. It will probably contain most small numbers, because if $x\in S$ then all divisors of $x$ need to be in $S$. On the other hand the larger numbers, those of an order of magnitude larger than $n$, must be rather sparse, because they need to have lots of common factors. Then, of course, there are no elements of $S$ above $9n^2$. To begin with, I want to take a closer look at this $S$ from the sparse side, namely down from $9n^2$.

Note: the choice of strategy just described is the key step to the solution. It came to my mind in a natural and, I should say, subconscious way. It is, however, interesting to spell out in words which choices have been made. First, I decided to fix the maximum lcm to $9n^2$ and try to look for the largest $S$ that fits, with a view, obviously, of proving that this $S$ has necessarily less than $6n$ elements, thus obtaining a contradiction. A symmetric approach, which we can call direct, would have been to fix the cardinality of $S$ instead of the largest lcm, and then prove that one of the lcms is $>9n^2$. In other words, one tactic is to fit as many objects as possible in a limited space, the other is to fit a fixed number of objects in the smallest possible space. I cannot offer a rational argument to justify my preference for the first, except, possibly, this: in an attempt to figure out which mechanism limits the space, it appears natural to just fill it up until whatever it is that becomes exhausted prevents further progress, thus making itself visible. Such a general consideration is not satisfactory, and, in other circumstances, I would probably just do it the other way round without giving much thought. The second choice is to look first at the largest numbers in this critical $S$. Why? It is obvious that the big end of $S$ is where the hypothesis that all lcms are $\le 9n^2$ imposes the most immediate constraints.

So I want to look just below $9n^2$. Clearly I cannot have two numbers $x$ and $y$ just below $9n^2$, because their lcm would be at least $2x$ or $2y$, and this is already too much. Indeed, this argument tells me that there is at most one number between $\frac{9}{2}n^2$ and $9n^2$. I paid one single number to halve the upper bound: that's good business in my book. I call $A$ the number $9n^2$, and I draw a picture like this

to signify that the interval between $\frac{1}{2}A$ and $A$ contains at most one element of $S$. Another one-element interval seems to be between $\frac{1}{3}A$ and $\frac{1}{2}A$, because two elements in there cannot differ only by a factor of $2$, thus the lcm is at least $3$ times one of them (actually even $4$ times maybe, but it's not time for fine tuning yet). My picture displays now more detail, and an obvious conjecture. 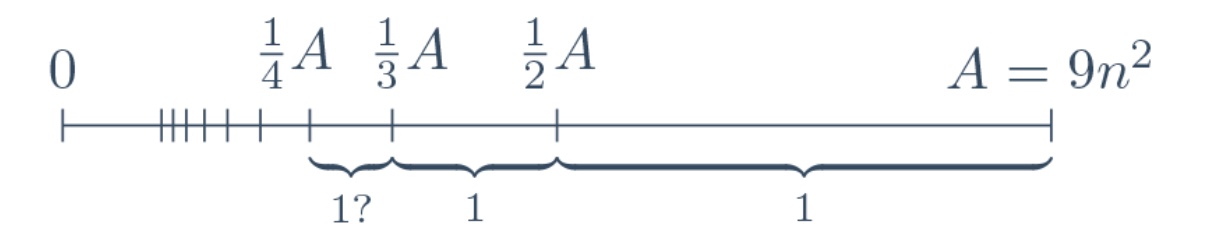Does the pattern continue? It seems so.

To state the last observation formally, it should happen that, for all $i\ge 1$, if $\frac{A}{i+1} < x < y \le \frac{A}{i}$, then $\operatorname{lcm}(x,y) > A$. Arguing about the common factors of $x$ and $y$ is cumbersome, so I would prefer to control the lcm somehow more algebraically. Considering that $x$ and $y$ are sandwiched in a small interval, there is an obvious upper bound on the gcd, namely the size of the interval. This calls for the well known relation connecting lcm and gcd \[ \operatorname{lcm}(x,y) = \frac{xy}{\operatorname{gcd}(x,y)} \ge\frac{xy}{y-x} > \frac{\left(\frac{A}{i+1}\right)^2}{\frac{A}{i}-\frac{A}{i+1}} = A \frac{i}{i+1} \]OK, I hoped to get $A$, but I got a little bit less (the fraction $\frac{i}{i+1}$ is quite close to $1$). Probably I just need to do my computation more carefully, because the claim itself, I already observed, wastes information. Yet it's promising enough. Before I spend more time fixing this argument, I prefer to assume the claim and see what benefit can be drawn from it. Joining the intervals, the claim tells me that there are at most $i$ elements of $S$ above $\frac{A}{i+1}$. Remembering that $A=9n^2$, it seems reasonable to try $i+1=\sqrt{A}=3n$, so $S$ has at most $3n-1$ elements above $3n$. Of course it also has at most $3n$ elements $\le 3n$, which makes $6n-1$. Here we go: the only missing step is the proof of the claim.

The computation above is patently very rough: I just replaced both $x$ and $y$ in the product $xy$ with their smallest possible value $\frac{A}{i+1}$, and then I replaced $y-x$ with the upper bound $\frac{A}{i}-\frac{A}{i+1}$. That's wasteful because $x$ and $y$ cannot be at the same time maximally small and maximally apart from each other. Let's try to keep $x$ and $y$ as indeterminates for a little longer \[ \operatorname{lcm}(x,y) \ge \frac{xy}{y-x} = \frac{1}{\frac{1}{x}-\frac{1}{y}} \]Now from the hypothesis $\frac{A}{i+1} < x < y \le \frac{A}{i}$, taking the reciprocals, I get \[ \frac{i}{A} \le \frac{1}{y} < \frac{1}{x} < \frac{i+1}{A} \;\;\Rightarrow \;\; \frac{1}{x}-\frac{1}{y} < \frac{1}{A} \]And, substituting in the formula above, $\operatorname{lcm}(x,y) > A$. Done.

It remains to collect the thoughts above and write up a formal solution, you will find it in the next section. The problem turned out to be much easier than expected, however I suspect that good luck helped me considerably. So always remember to throw gems at unicorns before contests. In hindsight, the large gap between part (a), $32n^2$, and part (b), $9n^2$, should have told me that there was no razor-sharp construction going on. On the other hand, I can only be grateful that it was so: this is a sort of problems where often one can make improvements by considering more and more intervals, and constructing proofs like that can be tedious.

Don't be put off if you encountered difficulties solving this exercise, the stats show that the best score obtained by any of the 87 participants is 3 points out of 7, and 69 persons didn't make any point at all. Comparison with the two official solutions shows that they are based essentially on the same mechanisms as ours. Both the official solutions, however, do part (b) through the approach that we called direct. There is a distinct smell of black magic around these solutions, which confirms, in my mind, the intuition that the approach by contradiction opposes fewer obstacles.

Solution to problem 3

Let $n$ be a positive integer.

1. Prove that there exists a set $S$ of $6n$ pairwise different positiveintegers, such that the least common multiple of any two elements of $S$ is no larger than $32n^2$.
2. Prove that every set $T$ of $6n$ pairwise different positive integerscontains two elements the least common multiple of which is larger than $9n^2$.

(a) Let $S$ contain precisely the positive even numbers $\le 8n$ and the odd numbers $<4n$, hence a total of $6n$ numbers. Let $x$ and $y$ be elements of $S$, we show that $\operatorname{lcm}(x,y)\le 32n^2$. In fact, if at least one of them is odd, then\[\operatorname{lcm}(x,y) \le xy < (8n)(4n) = 32n^2\]Otherwise\[\operatorname{lcm}(x,y) = \frac{xy}{\operatorname{gcd}(x,y)} \le\frac{xy}{2} \le \frac{(8n)^2}{2} = 32n^2\]This concludes part (a).

(b) Assume towards a contradiction that $\operatorname{lcm}(x,y) \le 9n^2$ for all $x,y\in T$: we will prove that $T$ has less than $6n$ elements. We claim that, for all $i\ge 1$, the set $T$ contains at most one element in the interval $I_i:=\left(\frac{9n^2}{i+1}, \frac{9n^2}{i}\right]$. Assuming, for the moment, the claim, $T$ has at most $3n-1$ elements in the interval $(3n,9n^2] = \bigcup_{i=1}^{3n-1} I_i$. On the other hand, all elements of $T$ must not exceed $9n^2$, and there are at most $3n$ elements $\le3n$, therefore $T$ can have at most $6n-1$ elements, hence the statement.

It remains to prove the claim. Let $\frac{9n^2}{i+1} < x < y \le \frac{9n^2}{i}$. Taking reciprocals we get \[ \frac{i}{9n^2} \le \frac{1}{y} < \frac{1}{x} < \frac{i+1}{9n^2} \;\; \Rightarrow \;\; \frac{1}{x}-\frac{1}{y} < \frac{1}{9n^2} \]hence \[ \operatorname{lcm}(x,y) = \frac{xy}{\operatorname{gcd}(x,y)} \ge\frac{xy}{y-x} = \frac{1}{\frac{1}{x}-\frac{1}{y}} > 9n^2\]It follows that $x$ and $y$ cannot belong both to $T$, and the claim is proven.

Continue to the next problem >