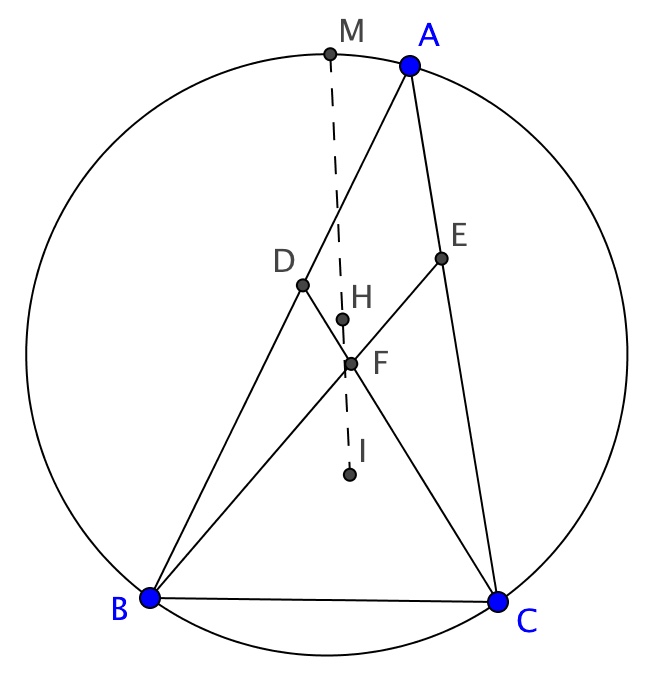
EGMO 2014, problem 2. Let $D$ and $E$ be points in the interiors of sides $AB$ and $AC$, respectively, of a triangle $ABC$, such that $DB=BC=CE$. Let the lines $CD$ and $BE$ meet at $F$. Prove that the incentre $I$ of triangle $ABC$, the orthocentre $H$ of triangle $DEF$ and the midpoint $M$ of the arc $BAC$ of the circumcircle of triangle $ABC$ are collinear.
 It is nice to sit in front of my pc and write this solution, remembering the first day of contest at my first EGMO, in Antalya, 2014.
It is nice to sit in front of my pc and write this solution, remembering the first day of contest at my first EGMO, in Antalya, 2014.
Needless to say, a large well-drawn figure is the first thing you need, when facing a geometry problem. It is usually a good idea to initially make a quick sketch of the figure in order to understand what adjustments can be taken to make the drawing clearer, and then draw the accurate final figure.
Now, let us analyze the first hypothesis: since $DB=BC=CE$, $CBE$ and $BCD$ are isosceles triangles. In particular $\angle BCD = \angle BDC$ and $\angle CEB=\angle CBE$. Along with highlighting equal angles with the same colour on the figure*, if it is easy as in this case, it may be a good idea to write the measures of the angles explicitly. Using the standard notation we have $\angle BCD = \angle BDC = 90 - \frac{\beta}{2}$ and $\angle CEB=\angle CBE = 90-\frac{\gamma}{2}$.
Since $I$ is the incentre of $ABC$ we have $\angle IBC=\frac{\beta}{2}$ and $\angle BCI = \frac{\gamma}{2}$. Now we see that having explicitly written the measures of the angles has proved to be useful: the presence of a $\frac{\gamma}{2}$ and a $90-\frac{\gamma}{2}$ reveals the existence of a right angle: defining $X = CI \cap BE$ and $Y=CD \cap BI$, we have $\angle CXB=90$ and similarly $\angle BYC=90$. We now look at the figure, and try to use all of the other hypotheses. $H$ is an orthocentre and we have just discovered two right angles, so let's work on this! Being $H$ the orthocentre of $DEF$, we have $DH \perp FE$ . We have just noticed that $FE \perp CI$, so lines $DH$ and $CI$ are parallel. Analogously, lines $EH$ and $BI$ are parallel. So we have now found the parallelogram $HSIT$, where $S = HE \cap CI$ and $T= BI \cap DH$. At this point of the contest I was happy because of the discovery of a parallelogram in my figure, but I then remained stuck for a while. I was looking at my well-drawn figure, but had some difficulties at finding an input for probably more than 20 minutes: I thus looked for some comfort in the cookies that I had found on my table at the beginning of the contest, and then decided to try to add something to my figure. When you are stuck, sometimes, it is worth it to work up the courage and define a new point or prolong a segment in order to find something new!
We would like to use that $M$ is the midpoint of arc $BC$. Since $M$ lies on the circumcircle of $ABC$, let's try to prolong the two couples of parallel sides of $HSIT$, and give a name to the intersections of this lines with the circumcircle. We define $J, R, Q, P, N, L$, as in the figure below, and also name the arcs: $CL =a, LN=b, NP=c, PM=d, MA=e, AQ=f, QR=g, RJ=h, JB=i$. Now that we have named them – and the figure has become a bit more threatening! – we should try to write some relationships among them. We are ready to use the information that $M$ is the midpoint of arc $BC$:
\begin{equation}a+b+c+d=e+f+g+h+i\tag{1}\end{equation}
Now, let's look for other relationships; $BI$ is the bisector of $\angle ABC$, then $N$ is the midpoint of the arc $AC$ not containing $B$, which leads to:
$$a+b=c+d+e\tag{2}$$
Analogously $R$ is the midpoint of arc $AB$:
$$f+g=h+i\tag{3}$$
Then, we can deduce another identity since the couple of lines $DH$ and $IC$ are parallel, and a couple of parallel lines cuts two equal arcs on a circle, so:
$$g=a\tag{4}$$
and analogously
$$c=i\tag{5}$$
Since we have written all of these equalities, we would like now to extract new information from them. Let us substitute (2) into (1), obtaining $2c+2d=f+g+h+i$. Using (3) we can rewrite the last expression as $2c+2d=2h+2i$, and using (5) this becomes $2c+2d=2h+2c \Rightarrow d=h$. This is good news, so it deserves to be highlighted in the figure. A dear friend of mine, Federica, who went to EGMO two years later, had given to me a set of felt-tip colours some weeks before I left for Antalya, saying "May these help you at EGMO when you will face the geometry problem!". They had actually brought me luck! I used the red felt-tip-pen to colour the two arcs on my figure.
Now, we have just used that a couple of parallel lines cuts two equal arcs on a circle, so we can now use this information in reverse: $RM$ and $JP$ are parallel. Let us explore the equations for another while: substituting $c+d=a+b-e$ in (1), we get $2a+2b-e=e+f+g+h+i$. Using again (3) this becomes $2a+2b=2e+2f+2g$, but since (4) holds, this becomes $b=e+f$. $e$ and $f$ are contiguous arcs on the circle, so we have just found another couple of congruent arcs, $QM$ and $NL$, that I highlighted in blue in the figure. We thus have another couple of parallel lines: $MN$ and $QL$. Now, since $MN$ is parallel to $HT$ and $HSIT$ is a parallelogram, we have $MN$ parallel to $RC$. Similarly, we have $MR$ parallel to $BN$. So, another parallelogram comes out in our figure: $RINM$.
We have two parallelograms, the small one and the big one, which share vertex $H$. To conclude that $I, H, M$ are collinear, we would like to show that there is an homothety of centre $H$ that maps $HSIT$ to $MRIN$ which is equivalent to showing that these two parallelograms are similar. This holds if and only if $\frac{IT}{IN}=\frac{IS}{IR}$. It is natural to use the chord theorem $IN \cdot IB=IR \cdot IC$, so we can rewrite the preceding equation, equivalent to the thesis, as $IS \cdot IC=IB \cdot IT$. This is what we would like to show to conclude the proof. This equation holds if and only if $SBCT$ is a cyclic quadrilateral. I remember I became a bit worried at this point, since I did not have much time left. Showing that a quadrilateral is cyclic can be done in many different ways, but just have a look at the figure: since $XBCY$ is clearly cyclic, we already have $\angle XBY= \angle XCY$. To prove that $BCST$ is cyclic it would be enough to show that $\angle SBT = \angle SCT$, which, after the last observation, is equivalent to proving that $\angle SBE = \angle DCT$. This seems a good way to proceed. Since $BCE$ is isosceles and $BE \perp CX$, then $CX$ is the axes of segment $BE$, so, since $S$ lies on $CX$, $SBE$ is also an isosceles triangle, and the same holds for $TDC$. In particular $\angle SBE = \angle SEB$ and $\angle TCD = \angle TDC$. The thesis is now equivalent to showing that $\angle SEB = \angle TDC$. This follows easily: let us define $O=DH \cap FE$ and $Z=HE \cap DF$. The quadrilateral $DZOE$ is cyclic since $\angle DZE= \angle DOE = 90$, because $H$ is the circumcentre of $FED$ and $O$ and $Z$ are the feet of two altitudes in this triangle. But then we have $\angle SEB = \angle ZEO =\angle ZDO = \angle CDT$, as we wanted to prove.
The contest ended a few minutes after I finished writing the last lines of the proof; I had liked the problem because of the number of nice intermediate steps that had led me to the conclusion. Since I was satisfied, I was then ready to spend a beautiful rest of day in Antalya with the other girls!
Here is Camilla's figure from Antalya!
