![]() English version below / Vai alla versione italiana
English version below / Vai alla versione italiana

To the layman mathematics often is an obscure and inscrutable exercise of sheer abstraction. The truth is, however, that a lot of deep and advanced mathematics is borne out of very simple and down-to-earth problems. The sphere packing problem is one of these.
Suppose, for instance, that a vendor has a certain quantity of oranges to be arranged in a box. What is the arrangement that maximizes the number of oranges that fit in a box? To give an abstract mathematical analysis of the problem one first has to make some simplifications, such as assuming the oranges are spheres of the same size, which is small compared to that of the box. The first thing one tries is to arrange some of them in a horizontal first layer, so that they form a lattice which has a honeycomb-like appearance, then a second layer on top of that where each sphere sits atop the hollows left in the lower layer, and so on. This is called the hexagonal close packing and fills up slightly more than 74% of the space (exercise: find the exact fraction!). However, another arrangement, the cubic close packing, attains this density, and many more which are significantly more irregular.

The question is then: can one obtain a better density than the one of the very simple hexagonal close packing? To get more insight into this, let us first look at a toy version, the two-dimensional problem (the one-dimensional problem being trivial: the spheres are segments and they fill up 100% of the space). Here, the optimal packing has long been known to be the one associated with the honeycomb lattice, achieving a density of more than 90%, from the works of Thue in 1910 and Fejes Tóth in 1943. In the 3D case, first posed by Kepler in 1611, the optimality of the hexagonal close packing has been finally proved by Hales in 1998 with a heavily computer-assisted proof. Before that, mathematicians already wondered what happens when packing spheres in dimensions higher than three. This is not an idle question for the sake of generalization–while no one of us is likely to eat a 10-dimensional orange anytime soon, packings in high dimensions are crucial to the construction of error-correcting codes. However, for dimensions beyond 3 very little is known in general, with the remarkable exceptions of dimensions 8 and 24. This is where today’s mathematician, Maryna Viazovska, enters the stage, having found a “stunningly simple” solution to the sphere packing problems for those two choices of dimensions.
Maryna Viazovska was born in 1984 in Ukraine. She got interested in mathematics during high school, thanks to the Mathematical Olympiads and to a science fiction book, whose main character was a mathematician. During her Bachelor in Kiev she was a participant and a first-award winner in the International Mathematics Competition for University Students as well. She then moved to Germany and obtained a master’s degree in Kaiserslautern, followed by a Ph.D. in Bonn, with a thesis titled Modular Functions and Special Cycles. As the title suggests, at the time, she was already interested in a kind of special functions occurring naturally in number theory, the so-called modular functions, and their applications to problems in other fields–modular functions play an important role in the theory of lattices. Her interests, however, are not limited to these topics: while still in Bonn, she, together with Bondarenko and Radchenko, solved a conjecture of Korevaar and Meyer on the existence of small spherical designs in arbitrary dimensions, a central problem in discrete optimization. After Bonn, she was a postdoc in Berlin and visited Princeton. It was in 2016 that her greatest achievement to date, the solution of the packing problem in eight dimensions, was accomplished, earning her the Salem Prize, the Clay Research Award, the SASTRA Ramanujan Prize, and the New Horizons Prize in Mathematics. She has been recently appointed full professor at EPFL Lausanne (Switzerland) and will be a Plenary Speaker at the International Congress of Mathematics, to be held in Rio de Janeiro.
Back to the sphere packing problem: in 2003, Cohn and Elkies showed that the 8D sphere packing problem could be solved, and the so-called E8 lattice packing would be optimal, if one could find a function with some very simple properties, which would certify the optimality of the upper bound previously known. This opened the way for Viazovska and her mastery of modular forms to attack the problem, but the problem of finding such a function resisted the attempt of other experts for several years. Modular forms are functions that possess special symmetries; they have been studied for centuries, and were central to Wiles’ proof of Fermat’s Last Theorem in 1994. They are intimately connected with lattices and their symmetries, which their connection to the packing problem. After some unsuccessful attempts with Bondarenko and Radchenko, in 2016 she finally managed to construct such a function, which surprised everyone in the field; the impressive feat was compared to those typical of the famous Indian mathematician Srinivasa Ramanujan, who notoriously came up with identities and functions no one ever dared to think about. Her construction is indeed very simple, compared with the complexity of the problem at hand. Not long after this breakthrough, she found together with Cohn, Kumar, Miller, and Radchenko the right function for the 24-dimensional problem, using similar methods.
When asked what her mathematical dream is, Maryna Viazovska answered in the European Women in Mathematics Newsletter that she would like to solve a problem nobody has thought of. “This is exactly what I find most inspiring in the history of mathematics: not when somebody solves a long-standing conjecture, but when somebody discovers a completely new direction or completely new phenomena that nobody had ever thought about before.” She says: “Think of when Grothendieck re-discovered algebraic geometry and put in a completely new setting, or think of the discovery of the fractals: in the mathematics that existed before there was simply no space for objects like these. Discoveries like these really change mathematics and the way we think about mathematics itself.” About women in mathematics, she acknowledges that women are still a minority in mathematics. She also remarks that the number of female mathematicians in European countries tends to vary. “The reason for that can’t be that mathematics is a masculine discipline because it is a universal science”, she says. At the moment, “the rules of the game for young scientists are not very family-friendly”, she says, “A family-friendly policy would benefit not only women but also men who are in academia and young people who want to pursue a scientific career.”
As a mother of 8-year-old boy, she admits that parents’ prejudices against girls still exist and she warns against their impact: “The general mindset for parents is that boys are supposed to be good at science and girls are supposed to be good at something else”, she says, “I find this attitude very harmful: when young adults choose a career for their future they don’t choose among all possibilities they have and don’t find what they can do best.” She continues, “I hear young parents like me saying things like ‘chess is very good for boys’. Why? Chess is good for both boys and girls as long as they like it. If your child is a boy it doesn’t imply he will be good at chess, and the opposite is also not true.”
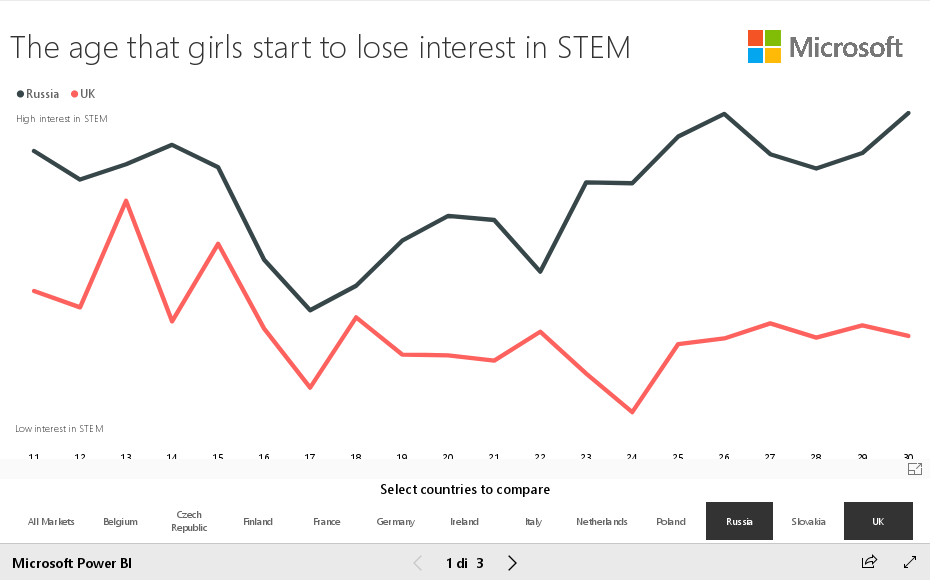
A recent survey by Microsoft seems to confirm Viazovska’s statements. According to the survey, most girls become interested in STEM at the age of 11 but this starts to wane by the age of 15. Parental expectations and the lack of female role models in STEM fields are cited among the reasons. As Viazovska remarked, the situation varies quite a lot from country to country, suggesting that cultural beliefs and societal expectations do play an important role. It is interesting to notice that Russian girls, in general, are more interested in STEM than the other European girls. The reasons for that seem to date back to the Soviet era, when scientific progress was a national priority and the government strongly encouraged scientific education for every kid, regardless of their gender. In the years of the space race, a significant fraction of engineers for the Soviet space program was composed of women, and female scientist role models were plentiful. Among the many, we recall the Soviet cosmonaut Valentina Tereskova, the first woman in space in 1963 (the USA sent their first woman into space, the astronaut Sally Reid, only twenty years later, in 1983). As of today, Russia has a remarkably high fraction of female researchers (41% vs. 29% worldwide, 15% of inventors against UK’s 4%) and does not experience any gender gap in technology. Similar trends can be spotted in many countries from the former Soviet Bloc, according to the UNESCO “Breaking the code” report. The results in mathematical competitions are witnesses to this as well, given for instance Ukraine’s track record at the EGMO. And Viazovska’s outstanding achievements in higher mathematics, fueled by her past Olympiad experiences, are no less remarkable.
![]() Versione italiana a seguire / Back to English
Versione italiana a seguire / Back to English

Alle persone comuni la matematica sembra a volte un esercizio di pura astrazione, oscuro ed impenetrabile - spesso assurdo. Tuttavia, la verità è che molta matematica profonda e avanzata nasce da problemi molto semplici e concreti. Il problema dell’impacchettamento di sfere è uno di questi.
Supponiamo che un fruttivendolo voglia sistemare una certa quantità di arance in una scatola: qual è la sistemazione che garantisce di poter sistemare il massimo numero possibile di arance? Per dare una formulazione matematica del problema dobbiamo prima fare alcune semplificazioni, come assumere che le arance siano sfere tutte della stessa taglia, che consideriamo trascurabile rispetto a quella della scatola. Il primo tentativo che si può fare è sistemarne alcune in un primo strato orizzontale, in modo che formino un reticolo a nido d’api, poi un secondo strato superiore dove ogni sfera è posta sugli avvallamenti lasciati nello strato inferiore, e così via. Questo è chiamato l’impacchettamento compatto esagonale e riempie poco più del 74% dello spazio (esercizio: trova la frazione esatta!). Un’altra sistemazione, l’impacchettamento compatto cubico, raggiunge anch’essa questa densità, e pure molti altri che sono molto più irregolari.
La domanda è quindi: è possibile ottenere una densità migliore di quella raggiunta dal molto semplice impacchettamento compatto esagonale? Per capirne di più, guardiamo prima a una versione giocattolo: il problema bidimensionale (quello unidimensionale è banale: le sfere sono segmenti che riempiono il 100% dello spazio). Qui l’impacchettamento ottimale è noto da tempo essere quello associato al reticolo esagonale, che raggiunge una densità di più del 90%, grazie ai lavori di Thue del 1910 e Fejes Tóth nel 1943. Nel caso tridimensionale, posto per primo da Keplero nel 1611, l’ottimalità dell’impacchettamento compatto esagonale è stato dimostrato essere il migliore da Hales nel 1998 con una dimostrazione che fa largo uso del computer. Prima di ciò, i matematici già avevano esaminato cosa accade quando si impacchettano sfere in dimensioni maggiori di tre; questa non è una domanda oziosa per puro scopo di generalizzazione – anche se nessuno di noi mangerà un’arancia 10-dimensionale nel futuro prossimo, impacchettamenti in dimensioni alte sono cruciali per la costruzione di codici di correzione degli errori. Per dimensioni maggiori di 3 si sa molto poco in generale, con le notevoli eccezioni delle dimensioni 8 e 24. È qui che entra in gioco la matematica di oggi, Maryna Viazovska, che ha trovato una soluzione “incredibilmente semplice” al problema dell’impacchettamento di sfere per queste due dimensioni.
Maryna Viazovska è nata nel 1984 in Ucraina. Si è interessata alla matematica durante le scuole superiori grazie anche alle Olimpiadi di Matematica e a un libro di fantascienza il cui personaggio principale è un matematico. Durante la laurea triennale a Kiev, è stata partecipante e vincitrice del primo premio nelle Competizioni Internazionali di Matematica per Studenti Universitari. Si è quindi trasferita in Germania e ha ottenuto la laurea magistrale a Kaiserslautern, seguita da un dottorato a Bonn, con una tesi dal titolo Funzioni modulari e cicli speciali. Come suggerisce il titolo, all’epoca era già interessata in un tipo di funzioni speciali che compaiono naturalmente in teoria dei numeri, le cosiddette funzioni modulari, e alle loro applicazioni a problemi in altri campi – le funzioni modulari occupano un posto importante nella teoria dei reticoli. I suoi interessi, tuttavia, non sono limitati a questi argomenti: durante il suo periodo in Bonn, insieme a Bondarenko e Radchenko, ha risolto una congettura di Korevaar e Meyer sull’esistenza di disegni sferici piccoli in dimensioni arbitrarie, un problema centrale in ottimizzazione discreta. Dopo Bonn, è stata post-dottoranda a Berlino e visitatrice a Princeton. Nel 2016 ha realizzato il suo più grande risultato finora, la soluzione del problema dell’impacchettamento in 8 dimensioni, che le è valsa il Premio Salem, il Premio di Ricerca Clay, il Premio Ramanujan SASTRA, e il premio New Horizons in Matematica. È attualmente professore ordinario all’EPFL di Losanna (Svizzera) e sarà conferenziere plenario al Congresso Internazionale dei Matematici 2018 a Rio de Janeiro.
Tornando al problema dell’impacchettamento di sfere: nel 2003, Cohn ed Elkies hanno dimostrato che il problema di impacchettamento in 8 dimensioni ammetteva una soluzione, e il cosiddetto impacchettamento regolare E8 sarebbe stato ottimale, se si fosse trovata una funzione con alcune proprietà molto semplici, che avrebbero attestato l’ottimalità di una maggiorazione nota in precedenza. Questo ha aperto la strada a Viazovska e alla sua padronanza delle forme modulari per attaccare il problema, che aveva già resistito ai tentativi degli esperti per diversi anni. Le forme modulari sono funzioni che possiedono simmetrie speciali; sono state studiate per secoli e sono state fondamentali per la soluzione di Wiles all’Ultimo Teorema di Fermat nel 1994. Sono strettamente collegate ai reticoli e alle loro simmetrie, da cui la loro utilità per il problema dell’impacchettamento. Dopo alcuni tentativi infruttuosi con Bondarenko e Radchenko, nel 2016 Viazovska è finalmente riuscita a costruire una funzione del genere, che ha sorpreso tutti nel campo; l’impresa è stata paragonata a quelle tipiche del famoso matematico indiano Srinivasa Ramanujan, che notoriamente trovava identità e funzioni che nessuno avrebbe mai osato immaginare. La costruzione di Viazovska è in effetti molto semplice rispetto alla complessità del problema in oggetto. Poco dopo la sua scoperta, lei ha trovato, insieme a Cohn, Kumar, Miller, e Radchenko, la giusta funzione per il problema in 24 dimensioni, usando metodi simili.
Alla domanda su quale sia il suo sogno matematico, Maryna Viazovska ha risposto alla European Women in Mathematics Newsletter che le piacerebbe risolvere un problema a cui nessuno ha pensato. “Questo è esattamente quello che mi ispira di più nella storia della matematica: non quando qualcuno risolve una congettura aperta da tempo, ma quando qualcuno scopre una direzione completamente nuova o fenomeni completamente nuovi a cui nessuno aveva pensato prima.” Spiega: “Pensate ad esempio a quando Grothendieck ha riscoperto la geometria algebrica e l’ha impostata in modo completamente nuovo, o pensiate alla scoperta dei frattali: nella matematica che esisteva prima semplicemente non c’era posto per oggetti come questi. Scoperte così cambiano davvero la matematica e il modo in cui pensiamo alla matematica stessa.” Riguardo alle donne in matematica, riconosce che le donne sono ancora una minoranza. Nota anche che il numero di donne matematiche nei Paesi europei tende a variare. “La ragione non può essere che la matematica è una disciplina maschile, perché è una scienza universale,” dice. Al momento, “le regole del gioco per i giovani scienziati non sono favorevoli alle famiglie”, dice, “un sistema adatto alle famiglie farebbe bene non solo alle donne ma anche agli uomini nel mondo accademico e ai giovani che vogliono intraprendere una carriera scientifica.”
Come madre di un bambino di otto anni, ammette che i pregiudizi dei genitori contro le ragazze esistono ancora e mette in guardia contro il loro impatto: “Il modo di vedere generale dei genitori è che i ragazzi saranno bravi nelle scienze e le ragazze saranno brave in qualcos’altro”, dice, “trovo che questo atteggiamento sia molto dannoso: quando i giovani scelgono una carriera per il loro futuro, non scelgono tra tutte le possibilità che hanno e non trovano quella che possono svolgere al meglio.” Continua: “sento genitori giovani come me dire cose come ‘gli scacchi sono ottimi per i ragazzi’. Perché? Gli scacchi sono un buon passatempo sia per ragazzi che per ragazze fintanto che a loro piacciono. Se tuo figlio è un ragazzo non vuol dire che sarà bravo negli scacchi, e anche il viceversa è falso.”
Una recente indagine della Microsoft sembra confermare le affermazioni di Viazovska. Secondo l’indagine, la maggior parte delle ragazze si interessano a materie scientifiche all’età di 11 anni ma questo interesse comincia a calare dai 15 anni. Le aspettative dei genitori e la mancanza di figure di riferimento nelle scienze compaiono tra le motivazioni. Come Viazovska nota, la situazione varia molto da paese a paese, cosa che suggerisce che i fattori culturali e le aspettative della società giochino un ruolo importante. È interessante notare che le ragazze russe, in generale, sono più interessate alle scienze delle altre ragazze europee. Le motivazioni sembrano risalire all’epoca dell’Unione Sovietica, quando il progresso scientifico era una priorità nazionale e il governo incoraggiava fortemente l’educazione scientifica di ogni adolescente, a prescindere dal genere. Negli anni della corsa allo spazio, una percentuale significativa di ingegneri del programma spaziale sovietico era composta da donne, e abbondavano i modelli da seguire nelle scienze. Tra le molte, ricordiamo l’astronauta sovietica Valentina Tereskova, la prima donna nello spazio nel 1963 (gli USA spedirono la loro prima donna nello spazio, l’astronauta Sally Reid, solo vent’anni dopo, nel 1983). Ad oggi, la Russia ha una percentuale notevolmente elevata di ricercatrici (41% contro la media mondiale del 29%, 15% delle inventrici contro il 4% del Regno Unito) e non vede alcun gender gap nella tecnologia. Andamenti simili sono visibili in molti Paesi dell’ex URSS, stando al rapporto UNESCO “Breaking the code”. I risultati nelle competizioni matematiche confermano anch’essi questo trend, dato ad esempio lo storico dell’Ucraina alle EGMO. E gli straordinari risultati di Viazovska in matematica, iniziati dalle sue esperienze alle Olimpiadi di Matematica, non sono da meno.