Blog

  English version below / Vai alla versione italiana

One of the greatest frustrations for many mathematicians, computer scientists and scientists is seeing themselves all too often represented in media and literature according to the outdated and unrealistic stereotypes of the “genius” and the “geek”.

The stereotype of “genius” was born in the Romantic period of the nineteenth century and depicts scientists as upper class European men, with a precocious innate talent and a sort of natural “vocation” for studies that manifests itself already at a very early age. More comfortable with books, formulae, and stills than with people, scientists are represented as lonely men, surly and very quirky, often mentally unstable. In the description of their research, the role of intuition - “genial”, indeed - is emphasized over that of orderly and patient study; the moment of “scientific discovery” is introduced as a “flash of ideas” that come sudden and unpredictably - as some sort of wizardry. This kind of narration is typical of E. T. Bell’s “Men of Mathematics” as well as of other famous fictional characters, like Professor Moriarty in A. Conan Doyle’s “Sherlock Holmes”, Hari Seldon in Isaac Asimov’s “Foundation”, or “Back to the Future”’s Doc Brown.

According to the “geek” model, on the other hand, mathematicians and scientists supposedly grow out of socially inept ex-teenagers. They are shy, unattractive, bad at sports, lovers of science fiction and fantasy; boring people without any interests outside science and technology, obsessed by their work. This stereotype crystallized in popular culture - especially in US/UK - starting in the ‘80s thanks to movies like “Revenge of the Nerds” or “Real Genius”; many characters from “The Big Bang Theory”, “Family Matters”’s Steve Urkel, or “The-40-Year-Old-Virgin”’s Andy Stitzer, all fit this kind of narrative.

We would like to emphasise to our readers that these are nothing but stereotypes: mathematicians and scientists are nothing but people doing mathematics and science. As such, they come in all shapes and sizes, with the most diverse interests, personal stories and temperaments!

Today’s mathematician, Miranda Cheng, is a very good example of how mathematics moves in mysterious ways.

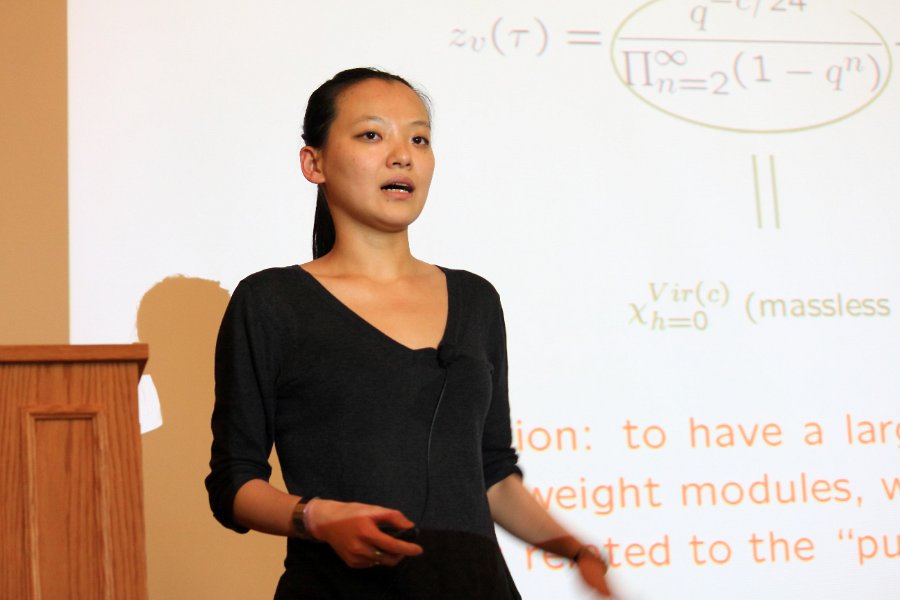
© Stony Brook University

Born in 1979 in Taipei (Taiwan), Miranda Cheng was a rebel girl. Keen on literature and music, she left school at 16 to play in a punk-rock band. She obtained a Bachelor’s degree in Physics at the National Taiwan University in 2001, then decided that she wanted to travel the world and she moved to Utrecht in the Netherlands. There she continued her studies, obtaining a Master’s degree from the University of Utrecht under the guidance of Nobel prize winner Gerard ‘t Hooft. Thanks to this experience, she decided to make a career out of research. She moved to the University of Amsterdam, where in 2008 she obtained a Ph.D. under the guidance of Erik Verlinde and Kostas Skenderis. She did a postdoc at Harvard University, then worked at the CNRS in France; since 2014 she is assistant professor at both the Institute of Physics and the Korteweg-de Vries Institute for Mathematics in the University of Amsterdam. She is an expert in string theory, a theory that lies between mathematics and theoretical physics.

String theory is an attempt to reconcile general relativity and quantum mechanics. According to this theory, which was born in 1960 and is still under development, matter is made up of one-dimensional objects, called strings. From far away, a string looks just like an ordinary particle, with a mass, a charge, and other properties that depend on the mode of vibration of the string. String theory describes how these strings move in space and interact with each other (much like so-called Feynman diagrams do for ordinary particles). Despite it being very difficult to verify experimentally, string theory is extremely interesting to mathematicians as a source of beautiful problems and conjectures. Among these, there are “Moonshine theories” - some unexpected connections between modular functions - which we have already seen here - and some “strange” sporadic symmetry groups - strange enough to deserve the epithet of “monstrous”. The idea of a link between those two worlds seemed, at first, so strange that the entire theory has been dubbed “moonshine”. Miranda Cheng became famous among experts thanks to her “umbral moonshine conjectures”, a series of conjectures that link string theory to sporadic groups.

Below you can find an abridged version of her interview to Quanta Magazine (you can read it entirely here) where she tells how she started and what mathematics means to her.

Have you always had a knack for physics and math?

As a child in Taiwan I was more into literature — that was my big thing. And then I got into music when I was 12 or so — pop music, rock, punk. I was always very good at math and physics, but I wasn’t really interested in it. And I always found school insufferable and was always trying to find a way around it. I tried to make a deal with the teacher that I wouldn’t need to go into the class. Or I had months of sick leave while I wasn’t sick at all. Or I skipped a year here and there. I just don’t know how to deal with authority, I guess.

And the material was probably too easy. I skipped two years, but that didn’t help. So then they moved me to a special class and that made it even worse, because everybody was very competitive, and I just couldn’t deal with the competition at all. Eventually I was super depressed, and I decided either I would kill myself or not go to school. So I stopped going to school when I was 16, and I also left home because I was convinced that my parents would ask me to go back to school and I really didn’t want to do that. So I started working in a record shop, and by that time I also played in a band, and I loved it.

How did you get from there to string theory?

Long story short, I got a little bit discouraged or bored. I wanted to do something else aside from music. So I tried to go back to university, but then I had the problem that I hadn’t graduated from high school. But before I quit school I was in a special class for kids who are really good in science. I could get in the university with this. So I thought, OK, great, I’ll just get into university first by majoring in physics or math, and then I can switch to literature. So I enrolled in the physics department, having a very on- and off-again relationship to it, going to class every now and then, and then trying to study literature, while still playing in the band. Then I realized I’m not good enough in literature. And also there was a very good teacher teaching quantum mechanics. Just once I went to his class and thought, that’s actually pretty cool. I started paying a bit more attention to my studies of math and physics, and I started to find peace in it. That’s what started to attract me about math and physics, because my other life in the band playing music was more chaotic somehow. It sucks a lot of emotions out of you. You’re always working with people, and the music is too much about life, about emotions — you have to give a lot of yourself to it. Math and physics seems to have this peaceful quiet beauty. This space of serenity.

Then at the end of university I thought, well, let me just have one more year to study physics, then I’m really done with it and can move on with my life. So I decided to go to Holland to see the world and study some physics, and I got really into it there.

You got your master’s at Utrecht under Nobel Prize-winning physicist Gerard ’t Hooft, and then you did your Ph.D. in Amsterdam. What drew you in?

Working with [’t Hooft] was a big factor. But just learning more is also a big factor — to realize that there are so many interesting questions. That’s the big-picture part. But for me the day-to-day part is also important. The learning process, the thinking process, really the beauty of it. Every day you encounter some equations or some way of thinking, or this fact leads to that fact — I thought, well, this is pretty. Gerard is not a string theorist — he’s very open-minded about what the correct area of quantum gravity should be — so I got exposed to a few different options. I got attracted by string theory because it’s mathematically rigorous, and pretty.

With the work you’re doing now, aside from the beauty, are you also drawn to the mystery of these connections between seemingly different parts of math and physics?

The mystery part connects to the bad side of my character, which is the obsessive side. That’s one of the driving forces that I would call slightly negative from the human point of view, though not the scientist point of view. But there’s also the positive driving force, which is that I really enjoy learning different stuff and feeling how ignorant I am. I enjoy that frustration, like, “I know nothing about this subject; I really want to learn!” So that’s one motivation — to be at this boundary place between math and physics. Moonshine is a puzzle that might require inspirations from everywhere and knowledge from everywhere. And the beauty, certainly — it’s a beautiful story. It’s kind of hard to say why it is beautiful. It’s beautiful not the same way as a song is beautiful or a picture is beautiful.

What’s the difference?

Typically a song is beautiful because it triggers certain emotions. It resonates with part of your life. Mathematical beauty is not that. It’s something much more structured. It gives you a feeling of something much more permanent, and independent of you. It makes me feel small, and I like that.

  Versione italiana a seguire / Back to English

Una delle più grandi frustrazioni per matematici, informatici e scienziati è quella di vedersi troppo spesso rappresentati nei media e nella letteratura secondo gli stereotipi antiquati ed irrealistici del “genio” e del “geek”.

Quello del “genio” è uno stereotipo che nasce nell'Ottocento durante il Romanticismo e dipinge gli scienziati come uomini europei di alta estrazione sociale, con un talento precoce innato e una sorta di “vocazione” naturale verso gli studi che si manifesta già in tenera età. Più a loro agio con libri, formule e alambicchi che con le persone, gli scienziati vengono rappresentati come uomini solitari, burberi e molto eccentrici, spesso mentalmente instabili. Nella descrizione della loro ricerca si enfatizza il ruolo dell'intuizione - “geniale”, appunto - rispetto a quello dello studio metodico e paziente; il momento della “scoperta scientifica” viene presentato come una successione di “lampi” di idee che arrivano improvvisi e imprevedibili - quasi una sorta di stregoneria. A questo tipo di narrazione si riconducono tutti i ritratti dei “Men of Mathematics” di E. T. Bell, nonché altri celebri personaggi come il professor Moriarty in “Sherlock Holmes” di A. Conan Doyle, Hari Seldon della trilogia della “Fondazione” di Isaac Asimov o Doc di “Ritorno al Futuro”.

Secondo il modello “geek”, invece, matematici e scienziati sarebbero per lo più ex-adolescenti socialmente inetti, timidi, poco attraenti, negati negli sport, amanti della fantascienza e del fantasy, persone noiose e senza interessi al di fuori della scienza e della tecnologia, ossessionati dal loro lavoro. Questo stereotipo si è cristallizzato nell'immaginario collettivo - soprattutto anglo-americano - a partire dagli anni '80 grazie a film come “La rivincita dei nerds” o “Scuola di geni”; in questo tipo di narrazione rientrano per esempio molti personaggi di “The Big Bang Theory”, Steve Urkel di “Otto sotto un tetto” o Andy Stitzer di “40 anni vergine”.

Ci teniamo molto a ricordare che questi non sono altro che stereotipi: matematici e matematiche, scienziati e scienziate non sono altro che persone che fanno matematica e scienza. In quanto tali, ce ne sono di tutte le forme e taglie, con gli interessi, le storie personali e i tratti caratteriali più disparati!

La matematica di oggi, Miranda Cheng, è un ottimo esempio di come le vie della matematica siano infinite.

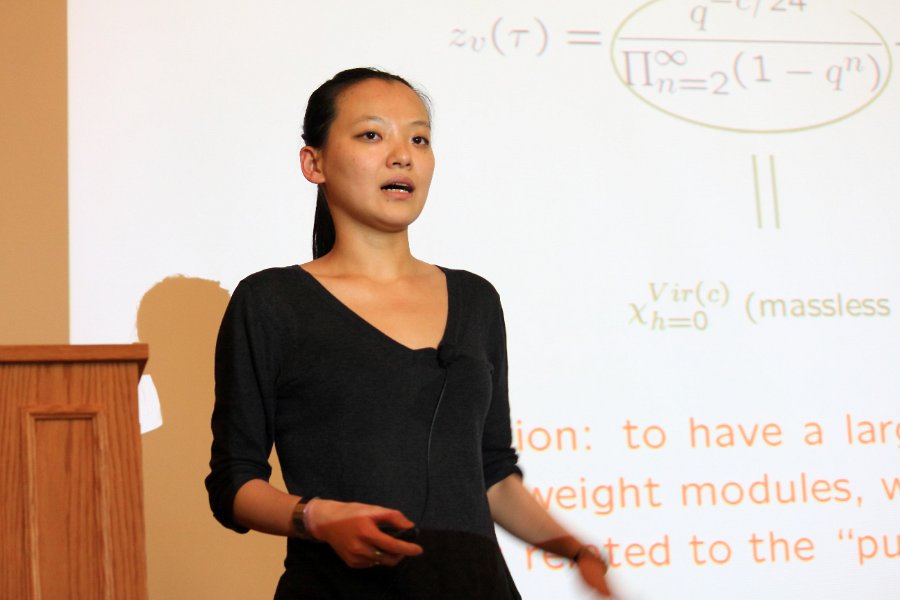
© Stony Brook University

Nata nel 1979 a Taipei (Taiwan), Miranda Cheng è stata una ragazzina ribelle. Appassionata di letteratura e musica, ha abbandonato la scuola a 16 anni per suonare con una band punk-rock. Consegue un Bachelor in Fisica alla National Taiwan University nel 2001, poi decide che vuole vedere il mondo e si trasferisce a Utrecht in Olanda. Qui continua gli studi, svolgendo un master alla Utrecht University sotto la supervisione del premio Nobel Gerard 'tHooft. Grazie a questa esperienza, decide di fare della ricerca la sua strada. Si trasferisce alla University of Amsterdam, dove nel 2008 consegue un Ph.D. sotto la supervisione di Erik Verlinde e Kostas Skenderis. Svolge un postdoc alla Harvard University, poi lavora al CNRS in Francia, dal 2014 è assistant professor all'Institute of Physics and Korteweg-de Vries Institute for Mathematics di Amsterdam. È un'esperta di teoria delle stringhe, una teoria che si sviluppa fra la matematica e la fisica teorica.

La teoria delle stringhe è un tentativo di conciliare la relatività generale e la meccanica quantistica. Secondo questa teoria, nata nel 1960 e ancora in fase di sviluppo, la materia è formata da oggetti uno-dimensionali, chiamate stringhe. A grandi distanze una stringa sembra una particella ordinaria, con massa, carica e altre proprietà che dipendono dallo stato di vibrazione della stringa. La teoria delle stringhe descrive come queste stringhe si propagano nello spazio e interagiscono fra loro. Malgrado sia una teoria ancora difficile da verificare sperimentalmente, è invece interessantissima per i matematici perché fonte di bellissimi problemi e congetture. Fra queste, ci sono le “teorie del chiaro di luna” - alcune inaspettate connessioni fra le funzioni modulari - di cui abbiamo già parlato qui - e alcuni “strani” gruppi di simmetrie - talmente strani da essere chiamati, appunto, “mostruosi”. L'idea di un collegamento fra questi due mondi è apparsa, in principio, talmente strana che l'intera teoria è stata battezzata “chiaro di luna” (moonshine). Miranda Cheng è diventata celebre fra gli addetti ai lavori grazie alle sue “congetture del moonshine umbrale”, una serie di congetture che legano la teoria delle stringhe ai gruppi sporadici.

Riportiamo sotto la traduzione di uno stralcio della sua intervista a Quanta Magazine (leggi per intero qui) in cui racconta come ha iniziato e cosa è per lei la matematica.

Ti sono sempre piaciute la matematica e la fisica?

Da bambina a Taiwan preferivo la letteratura - era quella la mia passione. Poi mi è presa quella per la musica a 12 anni circa - musica pop, rock, punk. Sono sempre stata molto brava in matematica e fisica, ma non sono mai stata davvero interessata. E ho sempre trovato la scuola insopportabile e cercavo continuamente un modo di evitarla. Ho cercato di convincere la mia insegnante che non avevo bisogno di andare a lezione. O facevo mesi di assenza per malattia quando in realtà non ero affatto malata. O saltavo un anno qui e li. Semplicemente non riuscivo a sopportare l’autorità, credo. E il materiale era probabilmente troppo facile. Ho saltato due anni, ma non è servito. Allora poi i hanno spostato in una classe speciale ed è stato semplicemente peggio, perché erano tutti molto competitivi e io non riuscivo a sopportare la competizione. Alla fine sono stata super depressa, e ho deciso che o mi sarei uccisa o avrei smesso di andare a scuola. Così ho smesso di andare a scuola a 16 anni, e me ne sono anche andata via di casa perché ero convinta che i miei genitori mi avrebbero chiesto di tornare a scuola e io davvero non volevo. Ho iniziato a lavorare in un negozio di dischi, e in quel periodo suonavo anche in una band, e lo adoravo.

Come sei arrivata da lì alla teoria delle stringhe?

Per farla breve, mi sono un po’ scoraggiata o annoiata. Volevo fare qualcos’altro oltre alla musica. Così ho cercato di tornare all’università, ma c’era il problema che non avevo il diploma di scuola superiore. Prima di lasciare la scuola, però, ero in una classe speciale per ragazzi molto bravi in scienze. Bastava per essere ammessi all’università. Così ho pensato, OK, ottimo, prima mi iscriverò a matematica o fisica, e poi passerò a lettere. Così mi sono iscritta al dipartimento di fisica, iniziando un tira-e-molla anche con questo, andando a lezione ogni tanto, e poi cercando di studiare letteratura, il tutto mentre ancora suonavo con la mia band. Poi mi sono accorta che non ero brava abbastanza in letteratura. E in più mi è capitato di avere un ottimo professore di meccanica quantistica. Mi è successo una volta di andare ad una sua lezione e ho pensato che fosse davvero roba figa. Ho iniziato a prestare più attenzione ai miei studi di matematica e fisica, e ho iniziato anche a trovarci la pace. È questo che ha iniziato ad attrarmi della matematica e della fisica, perché la mia altra vita nella band suonando musica era più caotica, in un certo senso. Ti succhia via un sacco di emozioni. Sei sempre a contatto con le persone, e la musica parla troppo della vita, delle emozioni - devi metterci dentro molto di te stessa. La matematica e la fisica sembravano avere questa bellezza pacifica e quieta. Questo spazio di serenità.

Hai ottenuto il tuo master a Utrecht con il premio Nobel Gerard ’t Hooft, poi hai fatto il dottorato ad Amsterdam. Cosa ti ha attirato?

Lavorare con [‘t Hooft] è stato un grosso fattore. Ma imparare di più è anche stato un grosso fattore - realizzare che ci sono così tante domande interessanti. Questa è la visione d’insieme. Ma per me è importante anche la parte giorno-per-giorno. La fase di apprendimento, la fase di pensarci, davvero la sua bellezza. Ogni giorni incontri delle equazioni o qualche modo di pensarci, o questo fatto porta a quel fatto - Ho pensato, beh, che è bello. Gerard non è un teorico delle stringhe - è davvero aperto su quale debba essere l’area corretta della gravità quantistica - così sono stata esposta ad alcune opzioni diverse. Sono stata attratta dalla teoria delle stringhe perché è matematicamente rigorosa, e bella.

Nel lavoro che stai facendo ora, a parte la bellezza, sei anche attratta dal mistero di questi collegamenti tra parti della matematica e della fisica apparentemente diverse?

La parte di mistero collega il lato cattivo del mio carattere, che è il lato ossessivo. È una delle forze guida che chiamerei leggermente negative dal punto di vista umano, ma non da quello dello scienziato. Tuttavia c’è anche una forza guida positiva, cioè che mi piace davvero imparare cose nuove e rendermi conto di quanto io sia ignorante. Mi piace provare quella frustrazione, tipo “Non so nulla di questo argomento; ho veramente voglia di impararlo!” Quindi questa è una delle motivazioni — essere al confine tra matematica e fisica. Il chiaro di luna è un rompicapo che potrebbe richiedere ispirazioni e conoscenze da qualunque parte. E la bellezza, senza dubbio — è una bella storia. È abbastanza difficile dire perché sia bella. È bella in un modo diverso da quello in cui una canzone è bella o un’immagine è bella.

Qual è la differenza?

Solitamente una canzone è bella perché scatena certe emozioni. Ti tocca a fondo. La bellezza matematica non è così. Ha molta più struttura. Ti dà una sensazione di qualcosa di molto più duraturo e indipendente da te. Mi fa sentire piccola e questo mi piace.